Circles - 8
Dumb Question. Why the equation of circle were taken to be x2 + y2 + 2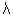
i x + a = 0 ? Where did the 'y' term went ?
Ans- Such equation of the circle can be taken if we chose the axis suitably .
The axis can be chosen as the nline joining the centre of two circles as x - axis and the point midway between the centre as origin.
And then we can obtain the equation as used in the question
(Q 1) Let AB be a chord of the circle x2 + y2 = r2 substens aright angle at the centre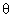
. Show that the locu of the coutroid of the triangle PAB as P mo ves on the circle is a circle.
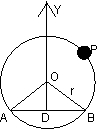
ODB is isosceles with OD = OB = x(say)
We may assume AB is parallel to and below x - axis .
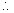x2 + x2 = r2=> x = r/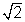
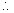B is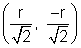 
and t is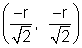 
Let P be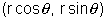
and centroid of PAB be G
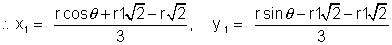
=> 3 x1 =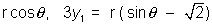
Eliminating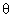, we get
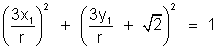
or x12 +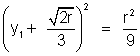
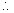Locus of (x1, y1) is circle
(Q Dumb question )
Why was x2 = r 2/2 implied
x = r 1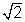
and correspondingly
A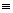
.
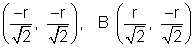(A) We have assumed OD as '+' ve y axis and OB '+' ve axis .
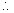x - co-ordinate of B is positive
x =
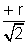and its y co-ordinate (iv)quadrent is below y - axis axis
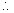B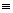 
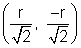
For A, x - co-ordinate on left of 0.
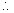x = 
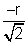, and its y - co-cordinate is '-' ve (i.e. (iii) quadrant)
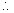A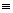 
.
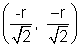(Q 2) The centre of circle S on use line 2x - 2y + 9 = 0 and cuts at right angles the circle x2 + y2 = 4 Show that S passes through two fixed point and find their co-ordinates.
(A 2) Let the circle S be : x2 + y2 + 2gx + 2fy + c =
centre lies on 2x - 2y + 9 = 0.
=> -2g + 2f + 9 = 0 .....................................(1)
S cuts x2 + y2 - 4 = 0 orthogonelly .
2g (0) + 2f (0) = c - 4 .
c = 4 - ........................................................(ii)
Using (i) and (ii) the equation of S becomes:
x2 + y2 + (2f + a) x + 2fy + 4 = 0
(x2 +y2 + 9x +4) + & (2x + 2y) =0
=> The circle S always passes through 2 fixed point A and B which are point of intersection of x2 + y2 + ax + 4 = 0 and 2x + 2y = 0
(as the above eqn can be compared to family circle S + KL = 0, where K is parameter).
Solving these eqn we get
x2 + x2 + 9x + 4 = 0
x = - 4, -1/2
y = 4 1/2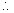 A 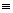(-4, 4), B (-1/2, 1/2)
Q3: The circle of X2+Y2-4X-4Y+4=0 is inscribed in atraingle has two sides long
the co-ordinates axes . the locus ofthe circumcenter of the traingle is x + y - xy + k
find the value of k.
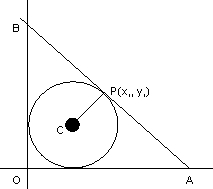
The given circle is (x-2)2+(y-2)2=4
=>centre=(2,2) and radius=2.
Let oab be the traingle in which the circle is inscribed. as
OAB is right angled, the circumcentre is mid point of AB. Let p=(x1,y1) be the circumcentre.
A=(2x,0) & B(0,2y1) THe eqn of AB is:,
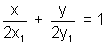
As AOB touches the circle, distance of AB=radius.
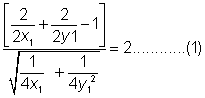
as the center (2,2) lies on the origin side of the line
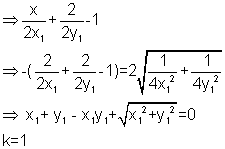
dumb question
(q) why is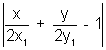
taken -
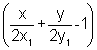lies on the origin side of the line
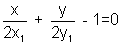
the expression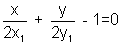 has the same sign as the constant term (-1) in the eqn-
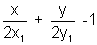is negative
Q4: Two circles each of radius 5 units touch each other at (1,2).if the equation of their common tangent is 4x+3y=10, find the equation of the circles.
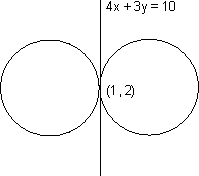
Equation of common tangent is 4x+3y=10. the 2 circles touch each other at (1,2)
. EQuation of family of circles touching a given line 4x+3y=10 at a given point (1,2) is
. (x-1)2+(y-2)2+k(4x+3y-10)=0,
x2+y2+(4k-2)x+(3k-4)y+5-10k=0
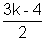and radius 2= g2+f2-c=(2k-1)2+(
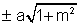)2-(5-10)
as the radius of the reqd. circle is 5
(2k-1)2+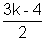-(5-10k)=52
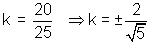
Put the values of k in 1 to get the Equation of reqd. circles
The reqd circles are
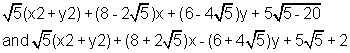
P is a variabe point on the line y=4.Tangent are drawn t the circle x2+y2=4 from p to touch it at A and B. the parallelogram. PAQB is completed. Prove that the locus of the point (y+4)(x2+y2)=2y2
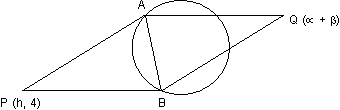
p lies on (y=4), then AB is chord of contact with respect to circle x2+y2=4 whose equation is
. hx + 4y = 4.........(1)
solving with circle we get
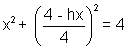
or x2(16+h2)-8hx-48=0
above gives abscissas of the point A And b,
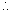x1+x2=
Also the points A and B lie on(1)
h(x1+x2)+ 4(y1+y2)=y+4
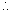4(y1+y2)=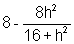
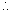y1+y2=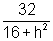
Now if the point q be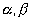
, then the figure PAQ being a paralelogram its diagnal bisect
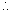x1x2=h+
=
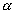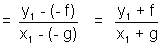......(2)
y1+y2=4+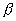
=
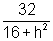
Now we have to eliminate the variable between(2) and (3) to find the locus of Q i.e,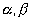
dividing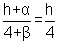
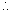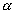4=h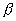
or h=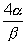
put in (3) and we get
(4+)(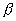
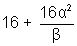)=32
locus is (y+4(x2+y2)=2y2
i x + a = 0 ? Where did the 'y' term went ?Ans- Such equation of the circle can be taken if we chose the axis suitably .
The axis can be chosen as the nline joining the centre of two circles as x - axis and the point midway between the centre as origin.
And then we can obtain the equation as used in the question
(Q 1) Let AB be a chord of the circle x2 + y2 = r2 substens aright angle at the centre
. Show that the locu of the coutroid of the triangle PAB as P mo ves on the circle is a circle.ODB is isosceles with OD = OB = x(say)We may assume AB is parallel to and below x - axis .
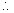x2 + x2 = r2=> x = r/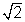 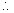B is 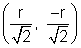and t is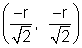 Let P be
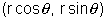and centroid of PAB be G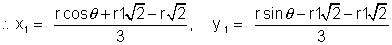 => 3 x1 =
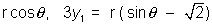
Eliminating
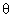, we get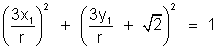 or x12 +
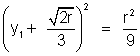
Locus of (x1, y1) is circle (Q Dumb question )
Why was x2 = r 2/2 implied
x = r 1
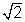and correspondingly A
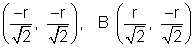.(A) We have assumed OD as '+' ve y axis and OB '+' ve axis .
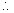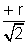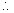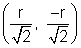
x - co-ordinate of B is positive x = and its y co-ordinate (iv)quadrent is below y - axis axis B For A, x - co-ordinate on left of 0.
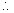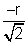x = , and its y - co-cordinate is '-' ve (i.e. (iii) quadrant) A 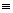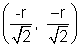.(Q 2) The centre of circle S on use line 2x - 2y + 9 = 0 and cuts at right angles the circle x2 + y2 = 4 Show that S passes through two fixed point and find their co-ordinates.
(A 2) Let the circle S be : x2 + y2 + 2gx + 2fy + c =
centre lies on 2x - 2y + 9 = 0.
=> -2g + 2f + 9 = 0 .....................................(1)
S cuts x2 + y2 - 4 = 0 orthogonelly .
2g (0) + 2f (0) = c - 4 .
c = 4 - ........................................................(ii)
Using (i) and (ii) the equation of S becomes:
x2 + y2 + (2f + a) x + 2fy + 4 = 0
(x2 +y2 + 9x +4) + & (2x + 2y) =0
=> The circle S always passes through 2 fixed point A and B which are point of intersection of x2 + y2 + ax + 4 = 0 and 2x + 2y = 0
(as the above eqn can be compared to family circle S + KL = 0, where K is parameter).
Solving these eqn we get
x2 + x2 + 9x + 4 = 0
x = - 4, -1/2
y = 4 1/2
A (-4, 4), B 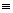(-1/2, 1/2)Q3: The circle of X2+Y2-4X-4Y+4=0 is inscribed in atraingle has two sides long
the co-ordinates axes . the locus ofthe circumcenter of the traingle is x + y - xy + k
find the value of k.
The given circle is (x-2)2+(y-2)2=4
=>centre=(2,2) and radius=2.
Let oab be the traingle in which the circle is inscribed. as
OAB is right angled, the circumcentre is mid point of AB. Let p=(x1,y1) be the circumcentre.A=(2x,0) & B(0,2y1) THe eqn of AB is:,
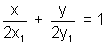
As
AOB touches the circle, distance of AB=radius.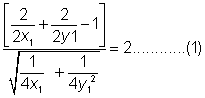as the center (2,2) lies on the origin side of the line
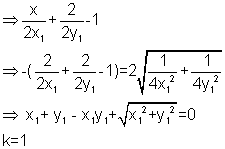
dumb question
(q) why is
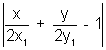taken - 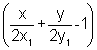lies on the origin side of the line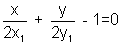the expression
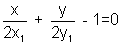has the same sign as the constant term (-1) in the eqn- 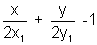is negativeQ4: Two circles each of radius 5 units touch each other at (1,2).if the equation of their common tangent is 4x+3y=10, find the equation of the circles.
Equation of common tangent is 4x+3y=10. the 2 circles touch each other at (1,2)
. EQuation of family of circles touching a given line 4x+3y=10 at a given point (1,2) is
. (x-1)2+(y-2)2+k(4x+3y-10)=0,
x2+y2+(4k-2)x+(3k-4)y+5-10k=0
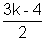and radius 2= g2+f2-c=(2k-1)2+(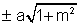)2-(5-10)as the radius of the reqd. circle is 5
(2k-1)2+
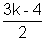-(5-10k)=52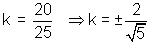Put the values of k in 1 to get the Equation of reqd. circles
The reqd circles are
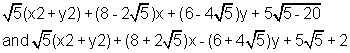
P is a variabe point on the line y=4.Tangent are drawn t the circle x2+y2=4 from p to touch it at A and B. the parallelogram. PAQB is completed. Prove that the locus of the point (y+4)(x2+y2)=2y2
p lies on (y=4), then AB is chord of contact with respect to circle x2+y2=4 whose equation is
. hx + 4y = 4.........(1)
solving with circle we get
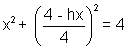
or x2(16+h2)-8hx-48=0
above gives abscissas of the point A And b,
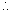x1+x2=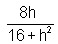Also the points A and B lie on(1)
h(x1+x2)+ 4(y1+y2)=y+4
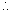4(y1+y2)=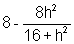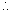y1+y2=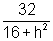Now if the point q be
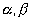, then the figure PAQ being a paralelogram its diagnal bisect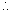x1x2=h+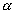=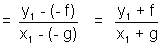......(2)y1+y2=4+
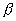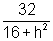
=Now we have to eliminate the variable between(2) and (3) to find the locus of Q i.e,
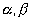
dividing
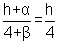
4=hor h=
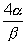put in (3) and we get(4+
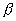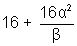)()=32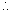 locus is (y+4(x2+y2)=2y2