Q11. find all common tangents to s1=x2+y2-2x-6y+9=0
S2=x2+y2+6x-2y-1
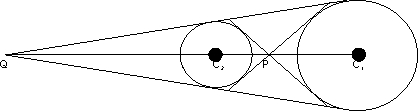
The centres and radii of the circles are c
1(1,3) and r
1=
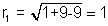
c
2(-3,1) and r
2=
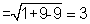Transverse common tangents are tangents drawn from the point p which divides c1c2 internally
in the ratio of radii 1:3.
Direct common tanent are tangents drawn from the point q which divides c1c2 externally in th ratio 1:3
co-ordinate of p are:
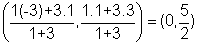
co-ordinate of q are:
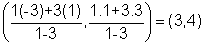
Transverse tangents are the tangents through any line through (0,5/2) is
(y-5/2)=mx or mx-y+5/2=0
apply the usual condition of tangency to any of the circle,
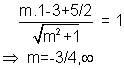
=> eqn of transverse tangents
3x+4y-10=0,x=0
direct tangents are tangents drawn from the p and q(3,4). let the eqn be (y-4)=m(x-3)
proceeding in same way,
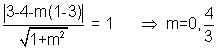
hence eqns of direct common tangents are
y=4,4x-3y=0
(Dumb question)
How does P and Q divide c1c2 externally and internally in the ratio r1:r2 and why in first case m is
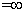
(for transverse tangents)
why?
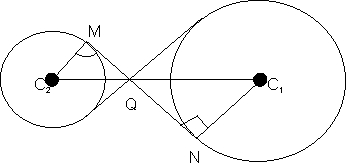
In
C
2MQ and C
1NQ
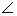
C
2mq=
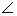
c
1NQ=90
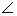
MQC
2=
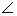
NQC
1(vertically opposite)
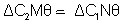
Hence,
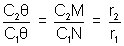
Now,(m
),
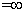
Eqn was
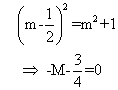
But since there are 2 values of m as there have to be 2 transverse tangents(isolated is not possible)
hence eqn is (o)m
2-m-3/4=0
Now product of roots
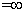
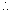
if one is real and finite other root is infinite
Find the interval of values of a for which t line y+x=0 bisects 2 chord drawn from point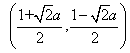 
to the circle
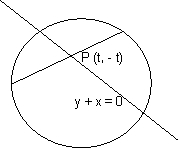
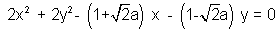
let m,n=
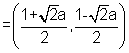
Equation of the circle reduces
x
2+y
2-mx-ny=0
let p(t,-t) be a point on the line y+x=0
Equatin of the chord passing through (t,-t) as mid -point
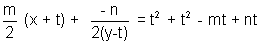
since chord (1) also passes through (m,n) it shows satisfy the equation of chord i.e
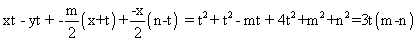
on substituting the values of m& n, we get
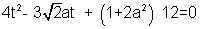
Now if there exists 2 chords passing through (m,n) and are bisected by the line y+x=0 then the equation of(2) should have real and distinct roots. D>0 => 18a
2-16(1+2a
2)/2>0
a
2-4>0=>(a+2)(a-2)>0
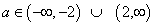
hence values of a are
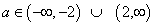
Q.3: the circle x2+y2 =1 cuts the x-axis at p and Q. another circle with center at Q and veriable redius intercept the first circle at R above x-axis and the line segment PQ at s. find the maximum of the triangle QSR.
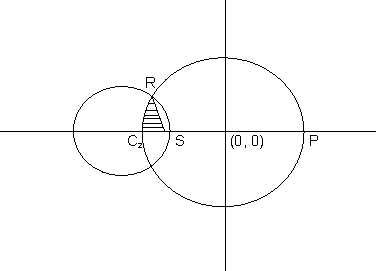
Equation of circle I is x
2 + y
2 = 1. it acts x-axis at point p(1,0) and Q (-1,0) Let the radius of the variable circle be r. center of the variable circle is Q(-1,0). Let the radius of the variable circle is (x+1)
2+y
2=r
2.........(2)
solving circle (1) and variable circle we get coordinate of r as
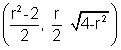
Area of the
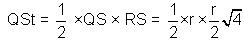
to maximise the area of the traingle to maximise the square,
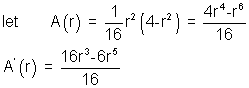
For A(r) to be maximum or minimum A'r=0
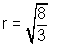
see yourself A''
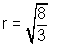
<0.
Area is maximum for
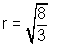
Maximum area of
QRS =
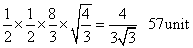
(Q.4) y = mx is a chord of the corcle of radius and whose diameter is along the axis of x. find the equation of the circle whose diameter is the chord and hence find the locus of center for all value of m.
Ans. The circle whose chordf is y = mx and center lies on x-axis will touch y-axis at origin. The equation of such circle is given by (x-a)
2 +y
2=a
2=>x
2+y
2-2ax=0.......(1)
furher family of circles passing through the intersection of circle (1) and the line y=mx is
x
2+y
2-x(2a+km)+ky=0
center of the circle is =(a + km/2.- k/2)
we require that the member of this family whose diameter is y=mx.
-k/2=am+km
2/2
=> k=-2ma/(1+m
2) => center of the requird circle lies on y=mx
Put the value of k in (1) to get the eqn of circle
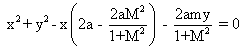
(1+m
2(x
2+y
2)-2a(x+my)=0........(2)
let the coordinate of the point whose locus is reqd. be (x1,y1)
=>(x1,y1) is the centre of the circle (2)
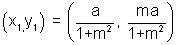
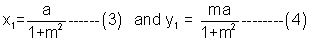
on squaring and adding (3) and (4) we get:
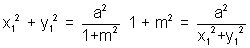
substituting the value of (1+m
2in (3) to get:)
x1
2+y1
2=ax1
required locus: x,sup>2+y
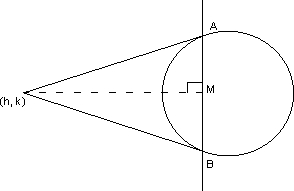
2=ax Tangents PA and PB are drawn from point (h,k) to the circle x
2+y
2=a
2
find the equation of circumcircle of
PAB and the area of
PAB
AB is the chord of contact for point p. Equation of ab is HX+ky=a
2
the circumcircle of
PAB passes through the intersection
of circle. x
2+y
2-a
2=0 and the line hx+ky-a=0
using s+kl=0, we can write the wequation of circle as: (x
2+k
2-a
2)+k(h
2+k
2-a
2)=0
=.k=-1
The circle is x
2+y
2-hx-ky=0
Area of
PAB= 1/2 PM X AB (PM is
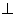
to AB)
PM= distance of p from AB
=
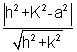
PA= length of tangent from p
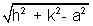
AREA=
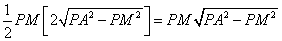
AREA=
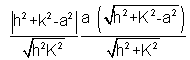
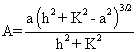
Note that h
2 + k
2 > a
2 (h, k) lies outside the circle. 1 center
2 circle
3 Radius
4 Diameter
5 Semicircle
6 Chord
7 Tangent
8 Normal
9 Chord of contact
10. External touch
11. Internal touch
12. point of contact
13. Direct tangent
14. Transverse Tangent
15. Concentric