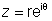Complex Numbers - 2
(2) Second Question : a < 0 , b < 0 then the principal value is arg (z)=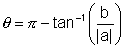 
is an obtuse angle & positive.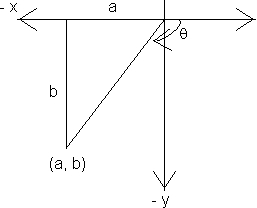
(3) a < 0, b < 0 then the principal value is argz =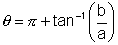 
is an obtuse angle & negative
(4) fourth Question : a > 0, b < 0 then the principal value is arg (z) is an acute angle & negative
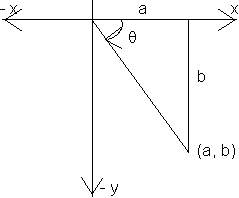
Dumb Question:- Find the modulus & amplitude of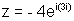 
(a) - 4, 3i (b) 4, 3i (c) + 4, 0 (d) 4e-3,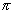 
Ans:
At first sight it looks like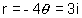 
, but modulus can’t be negative & also 
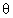can’t be imaginary so to make modulus positive we write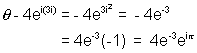
Now comparing with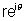 
we get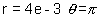 
ILLVATRATION - 2. What does arg (z) =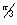 
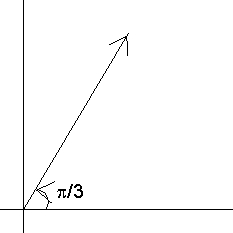
arg(z) = 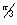shoues that Z is in first Quadrant & join of Zwith origin makes an angle of 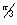with positive direction of x axis. Hence of Z is an open ray as shown in figure
CONJUGHTE OF A COMPLEX NUMBER
The complex number of z=a+ib &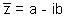 
are called complex conjugate of each other. The complex conjugate is obtained by changing the sign of imaginary part.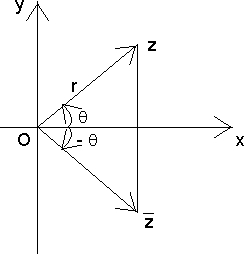
In polar from complex conjvgates are having same modulus & modulus of angle is same but the Angles differ in sing,
PROPERTIES OF CONJUGATE
(1) 
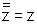
Why ?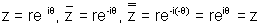 
(ii)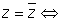 
z is purely real (both sided equality)
Why ?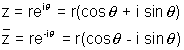
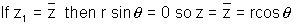ie purely real
(iii) 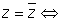is purely imaginary
Why ? if z = ki
then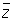 
= - ki Hence z = -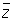
(iv)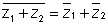
Why ? Let z1 - a1 + ib2
then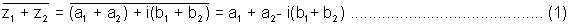 
& 
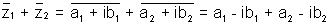
clearly (1) = (2)
(v)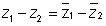 
(vi)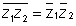 
Why ? Let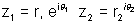 
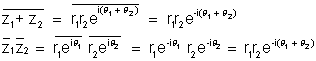
(vii)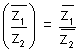 
(viii)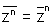 
Why ? Let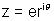
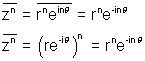
PROPERTIES OF MODULUS
(i)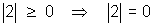 
& if (iff) z = 0
Why? |2| = r = distance of any point from orgin & distance can’t be negative.
(ii)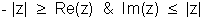 
Why ? Re(z) = r cos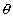
Im(z) = r sin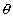
So,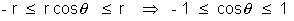 
which is true.
(iii)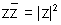 
(most important & frequently used property)
Why ?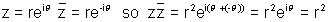 
(iv)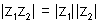 
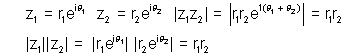
(v)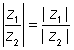 
(vi)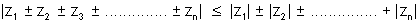 
(viii)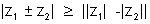 
When point z is joined kto origin O then the vector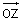 
can be used to represent complex
number z. We know that in a triangle sum of two sides is always greater thann third side. By using this concept the above property will be proved.
In figure 1: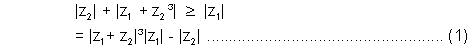
Dumb Question:- What happens when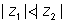 
Ans:- By same way we can also prove that
combining both (1) & (2)we can write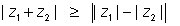
In figure2: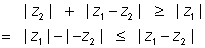
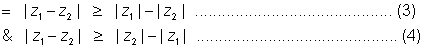
BY (3) & (4)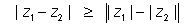
(viii)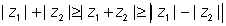 
Why ? Look at figure 1 of last property
we can writ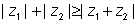 
because sum of two sides of triangle is greater than third side.
Modulus is always +ve. hence we can write.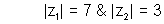
Then 
& 
Hence 
Dumb Question:- How can you kget eqn(7)from eqn(5)& 6 ?
Ans: suppose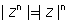 
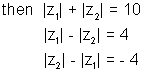
Hence 10 > 4 & nalso 10 > -4
If 10 > 4 it is obviously reater than - 4 but when we can use eqn. (7) to make sure that we compare + ve quantitics.
(ix)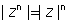 
Why? Let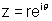 
then L.H.S.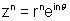 
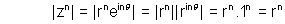
R.H.S.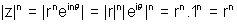 
Dumb Question: Why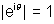 
?
Ans:- We know that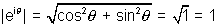 
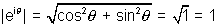
why ? By one of the previous properties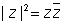
using this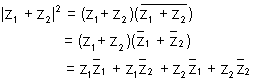
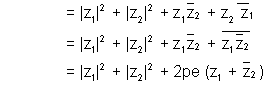
Dumb Question: Why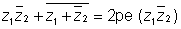 
we know that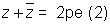 
here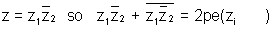 
PROPERTIES OF ARGUMENT
(i) Arg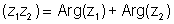 
Why ? Let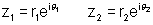 
then L.H.S>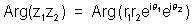 
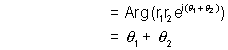
R.H.S.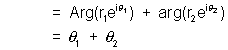 
s (ii) Arg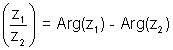 
(iii) Arg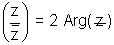 
Let 