Why? L.H.S.
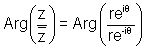
R.H.S.
(iv) Arg
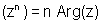
Why ? Let
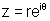
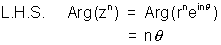
(v)
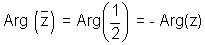
Why ? Let
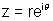
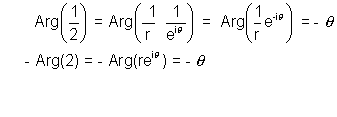
(vi)
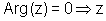
is purely real
Why ?
If
i.e. purely real.
(vii )
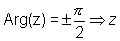
is purely imaginary
Why ?
If
= ri & -ri
Hence purely imaginary either ri or -ri
ILLUATRATION - 3.
Show that
[conj(arg(i)) + i arg(conj(i))] + [conj(arg(-i)) + i arg(conj(-i))] = 0
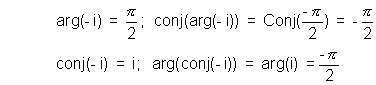
Using above four results we get
DE - MOIVRE'S THEOREM
The theorem states that for any
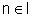
, we have
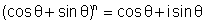
Why ? Let
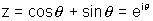
L.H.S. then
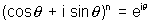
& we know taht
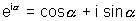
R,H.S. Hence
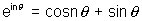Illustration :-
Suppose
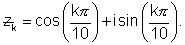
So,now find the value of
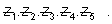
s
Ans:- Now suppose some
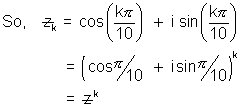
(Using De Movire's Theorem)
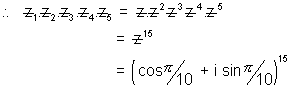
Now again using De Moviec's theorem.
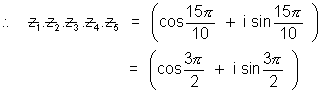
CUBE ROOTS OF UNITY.
Cube roots of unity means
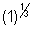
Lrt one of cube root of unity b x ,then.
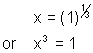
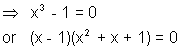
Solution of this cubic equation will give us three cube roots of unity.
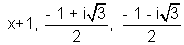
Let us call
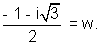
Now,
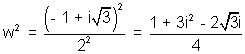
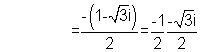
Therefore 3 cube roots of unity are 1, w, w
2.
ss
Dumb Question:- Why there are 3 solutions ?
Ans:- By theory of equation we know that a mnth orider equation will have n solution. Here n is 3 solution
PROPERTIES OF CUBE ROOT OF UKNITY.
1. 1 + w + w
2 = 0
Why? By theory of equation we know that for any nth order equation, sum of roots =
Here for x
3 - 1 = 0 , Sum
Why ? : Again by the theory of Equation product of roots
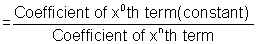
For x
3 - 1 = 0 we have
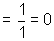
So product of roots 1, w, w
2 = 1.w.w
2 = w
3
Hence w
3 = 1. Now if w
3 = 1
Now if n
th the Taking nth power on both sides we get (w
3)
n = 1
n gives w
3n = 1.
3.
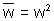
Why : By one of the properties we know that
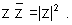
Hence z = w.
So
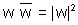
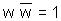
Hence
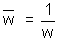
We also know that w
3 = 1 &
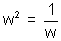
Hence
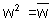
Dumb Question : How can you say taht |w| = 1
Ans : We know that w is cube root of unity . Hence
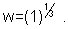
Taking modulus on both side we get
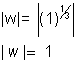
If w is a cube root of unity then find the value
Ans: (i)
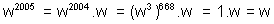
(ii)
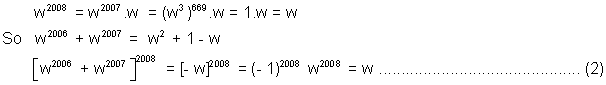
(iii)
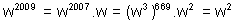
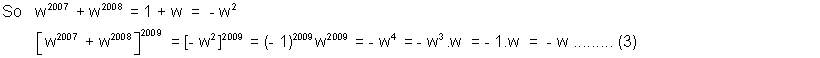
By (1).(2)& (3)
- 1 + w - w = - 1
Hence value is -1