Complex Numbers - 4
THE nth ROOTS OF UNITY
(1) The term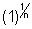 
is called nth root of unity
Let x = 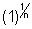be all possible nth roots of kunity
so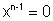 
is the equation whose solutions are n nth roots of unity.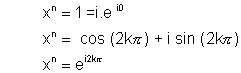
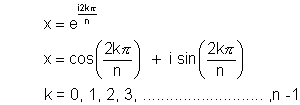
(2) The nth roots of unity form a G.P. & their sum is
Why:- For k = o x = 1
For k = 1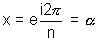 
For k = 2
For k = 3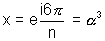 
For k = n -1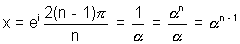 
Sum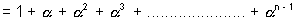 
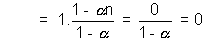
(3) The nth roots of unity can be represented on a unit circle . The points represented by n nth roots form a n sided polygon (regular) having centre at the origin. Having on vecter on positive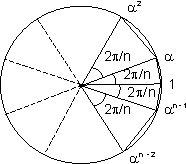
(4) From the above figure we can say that in the n nth roots of unity, both members of complex conjugate pair are the roots. The product of the n nth roots is.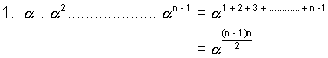
product of roots =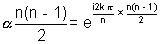 
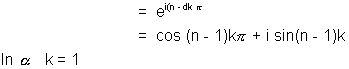
product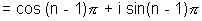 
= -1 if n is even , 1 if n is odd
Dumb Question:- How can we say that in n nth roots of unity both mamber of complex conjugate pair are the roots.
Ans:- Well the polygon that is drawn in point (3) is a regular polygon and it starts with the real axis . Now the two roots of the either side of real axis are poaced similarily because the angle they make with the real axis is same and both lie on unit axis so, such pairs are conjugatre of each other. Oone can go taking such pairs which well be conjugate of each other.
Illustration:-
If 
are n nth roots of unity. Find the value of 
Ans:- We know the equation whose roots are n nth roots of un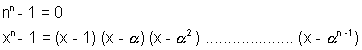
Replacing x as 6 we get
Hence Value of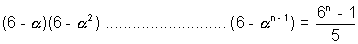 
ROTATION THEOREM (CONI METHJOD)
If z1, z2, z3 the vertices of triangle ABC desxibed in COUNTERCLOCKE sense then.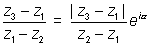
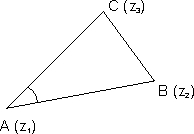
Why?
Let us shift the origin to prove this theorem . Let the origin be at z1.
By looking at above figure we can say that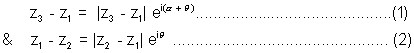
Dividing equation (1) by (2) we get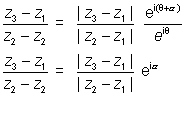
We can also say that Arg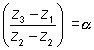 
Illustration - 6. If z1, z2, z3 are the vertices of equilaleral triangle. then find a relation between Z1, z2, z3?
Ans. Applying rotation theorem taking origin as z2 we get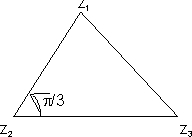
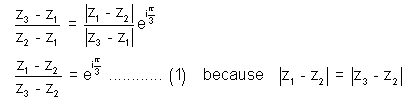
Again applyin Theorem now taking center a z1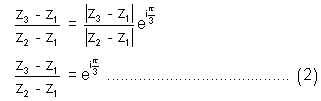
Equating (1) & (2)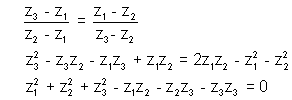
(1)Equation of a straight line through z1& z2is given by.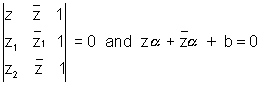
where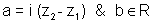 
Why ?
Let us apply Rotation theorem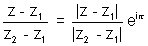
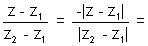A purely Real Number
solving we get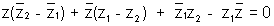 
Here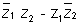
is purly imaginary . Let i + be ib, be,br />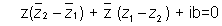
this can also be writen as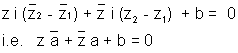
where a = i(z2 - z1) &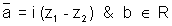 
(2)Slope of line segment joining any two points is given by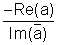 
Why?
eqn of line is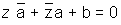 
Let z = x + iy & replacing kin this equation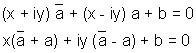
As we have in cartesion cooedinate system here also the slope is 
3) Equation of perpendicular Bisector jonining A(z1) & B(z2) is given by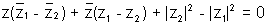 
Why?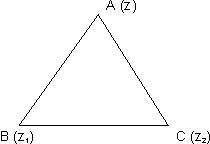
Consider a point c lying on the perpendicular bisctor of A & B then we have AC = AB
then we have AC = AB
i.e. | z - z1| = | z - z2|
Squaring both sides we get
|z - z1|2 = |z - z2|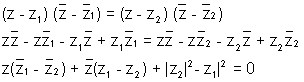
ILLUSTRATION:- Show taht thepoint z 2 is the reflection of line z1 in the line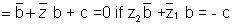 
Ans. If z 2is reflection of z 1 throught line . So the midpoint of AB lies on line i.e.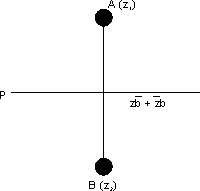
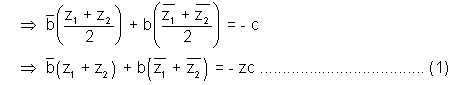
And also PO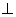 
AB, therefore, Slope of PQ = - Slope AB
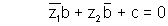
EQUATION OF A CIRCLE
The equation of a circle whose centre is z0 has radius r is |z - z0| = r |z - z0| < r represent the interior of circle & |z - z0| > r represent the exterior of circle.
Why?
Let z be any point on circle & we know that distance between any point & centre is r . So |z - z0| = r , Squaring both sides
|z -z0|2 = r2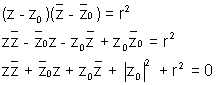
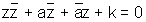where a = - z0 & k = |z0|2 Represents circle with centre - a & radius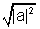 
EQUATION OF PARABOLA
Equation of parabola whose focus is at z0 & the line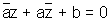 
is the directrix is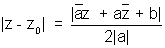
Why ?
By the definition of parabola we know that distance of any point on parabola to directic & focus remains same. So using that Distance betweet directrix & any point z = |z - z0| Distance between directrix & any point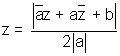 
Hence by equating we get the required Equation
ILLUSTRATION - 8.
find the centre & radius of circle given by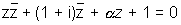 
Ans:- Comparing this with eqn of circle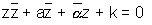 
we get a =1 + i & k = 1
a = - z0 centre of circle = - (1 + i)
K = |z0|2 Hence 1 = 2 - r2
r2 = 1, r = 1 is the radius of circle
Equation of elipse whose foci are z1 & z2 is |z - z1| + |z - z2| = 2a where 2a > |z1 - z2|
Why
From the definition of Elipse we know that the distance of any point on Elipse from two fixed point is constant & is 2a. So we can write the equation as |z - z1| + |z - z2| = 2a
EQUATION OF HYPERBOLA
Equation of hyperbola having foci at z1 & z2 is given by |z - z1| - |z - z2| = 2a where 2a is +ve real number & 2a < |z1 - z2|.
