Complex Numbers - 6 · KnowledgeBin.org

since z² + 4 is a quadratic expression we get a Linear remainder so
f(z) = g(z)(z ² + 4 ) + az + b
We have f(2i) = i = 0 + 2ia + b ………………………………………… (1)
f(-2i) = 2i = 0 + (-2i)a + b …………………………………………… (2)
Solving equation (1) & (2) we get

Hence the remainder is az + b
i.e.

Q. 5. If z is unimodular & then prove that (n amp(z))
Ans:- If z is unimodular let z =
then

Hence

Q.6. Prove the if
Ans:- We can write

We can also

Squaring eqn. (1) we get

Take

Now write & we get

Q.1. Find all the circle which are orthogonal to |z| = 3|z - 1| = 4

Ans:-

We have to find out the circles which are orthogonal to above these two circles i.e. tangents at the point of contact are at right angle to each other we know that
r₁² + r₂² = (C₁C₂)² (Applying pythogorus Theorem in PC₁C₂
Let the circle cuts orthogonally to |z| = 3 then

Also given that circle cuts |z - 1| = 4 orthogohally . so

Now

So we can write where + is any variable which corresponds to all the circles of family
Hence the requred equalion for family curves is

&

Hence K² = t²
equation is

Q.2. Solve equation z¹⁴ - 1 = 0 & deduce taht

Ans:-

k = 0, 1, 2, ………………….. , 13 are the roots of equation.
So roots are
Hence we can write

Diuiding both sides by z we get

Now put

We know that
If the prove the points representing 4 complex number in Argand plane are concyclic .

Ans:- Let
We get
Let
Now

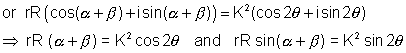
Squaring and adding, rR K² …………………………………………… (1)
Dividing, we get,

Let equation of circle passing through
Now , satisfy the equation.
So, we have,

Adding (3) and (4),we get

s And therefore,

(By using (2))

Taking conjugate , we get

By adding (7) and (8) we get

Put these values in (5) to get

(from (6))

Thus also satisfies the equation of circle.
Hence the problem.

Dumb Question:- How can we assure that circle passes through
Ans:- Well when three pointin a plane are given a unique circle passing through those 3 point can be trawn and here
is that circle only.