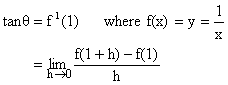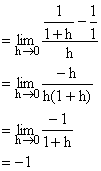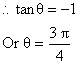differentiation-1

For many years the path in which planets were revolving round the sun was not known. After many years of observation Kepler conducted that planets move around the sun in elliptical orbits. But he could not give logical reasoning for his claim. But once Newton and Leibniz gave the fundamental theorem of calculus, the reasoning for this and many more things became quiet clear. Since then differential calculus has proved itself to be indispensable in development of mathematics and physics sciences.

In this section we will talk about some techniques of differentiation and their application to various question

 

So let us start with DIFFERENTIATION.

 

 

 

 

Definition of Derivative:

The derivative f¹(x) of a function y = f(x) at a given point x is defined as

Where f¹(x) is called derivative of f(x) with respect to x.

 

Derivation of f(x) from first principle (i.e. Definition on ab-init):

Let y = f(x) for an increment dx in x, let dy be the corresponding increment in y.

y + dy = f (x+dx).

      dy = f (x+dx)-f(x)

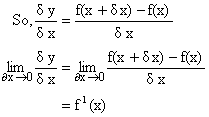
f¹(x) if exists is called derivative of f(x) w.r.t x.

Note: all represents the same thing.

Illustration 1:

Find the derivative of  w.r.t x using the first principle?

Solution:

Let y =

 

 

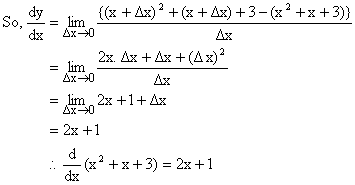
Right and Left Derivative of a function:

The Right hand derivative of a function at point ‘a’ denoted by is defined as

Similarly left hand derivative of function at ‘a’ denoted by is defined as

Differentiability of a function at a point:

A function f(x) is said to be differentiable at a point ‘a’ if

1) Both and are exist and are finite.

2) = .

Illustration 2:

Prove that function |x-1| is not differentiable at x=1.

Solution:

Let us find the right hand derivative and left hand derivative of this function.

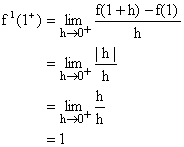
Similarly

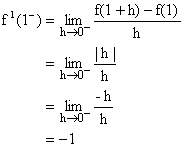
Now since , so the function is not differentiable at x = 1.

 

 

Geometrical Interpretation of a Derivative:

Let us take two point P[c, f(c)] and Q[c+h, f(c+h)] on curve y = f(x).

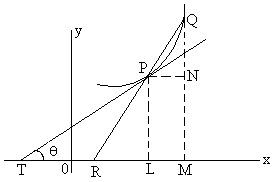
                        Fig (1)

We join PQ so that it is a secant to curve.

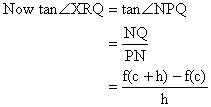
Now as h approaches O the point Q moving along curve approaches point P, the chord PQ approaches tangent line TP and ÐXRQ approaches ÐXTP denoted by Q.

Hence f¹(c) is slope of tangent to the curve y = f(x) at point (c, f(c)).

Illustration 3:

Show that tangent to hyperbola at (1, 1) makes an angle with x-axis.

Solution:

Let the angle the tangent makes beq.

So, we know that