differentiation-2
Derivability of f(x) on an interval
f(x) is said to be derivable on the closed interval [a, b] if
1) For the points a and b, ![]() , and
, and ![]() finitely exist.
finitely exist.
2) For any point c such that a<c<b, ![]() and
and ![]() finitely exist and equal.
finitely exist and equal.
3) f(x) is said to be derivable on open interval (a, b) for any point c such that a<c<b,
![]() And
And ![]() finitely exists and are equal.
finitely exists and are equal.
Illustration 4:
Consider the function;

Discuss differentiability of g(x) in [-1,¥].
Solution:

So, g(x) is not differentiable at x=1.
Relationship between continuity and differentiability:
If a function f is differentiable at a point ‘a’ then it is continuous at that point but if a function f is continuous at a point ‘a’ then it need not necessarily be differentiable at that point.
For Example:
y = |x| + 1 is continuous at x=0 but not differentiable.
Dumb Question:
1) How do we know that |x|+1 is not differentiable at x=0?
Ans:
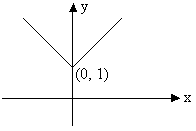
Fig (2)
The graph of function y = |x| + 1 looks like the figure mode above.
Now remember that derivative of a function represents the slope of graph at that point. So if there is no tangent line at certain point, function is not differentiable at that point or in other words function is not differentiable at corner point of a curve. And hence not differentiable at x=0.
Tips to check differentiability and continuity:
1) It is advantageous to check differentiability first because every differentiable function is continuous.
2) On the other hand every discontinuous function is non-differentiable.
3) If right hand derivative is not equal to left hand derivative but both exist finitely at x=a then function is not differentiable but continuous at x=a.
4) Continuity of a function does not imply its differentiability.
5) Also, non-differentiability of a function does not mean that it is discontinuous at point a.
Illustration 5:
Function f is defined by;
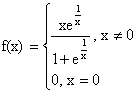
Show that f is continuous but not derivable at x=0.
Solution:

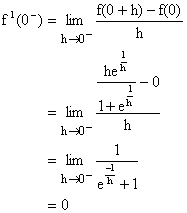
![]() So, f(x) is not derivable at x=0.
So, f(x) is not derivable at x=0.
But since both ![]() and
and ![]() exist finitely the function is continuous at x=0.
exist finitely the function is continuous at x=0.
Dumb Question:
1) Why 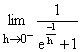 is 0 and
is 0 and 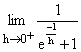 is 1?
is 1?
Ans:
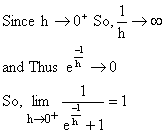
But when ![]() and thus
and thus
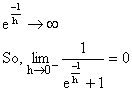
General Theorem on Differentiation:
1) ![]() (Constant) = 0 why?
(Constant) = 0 why?
Proof: Let f(x) = k.
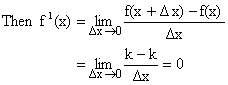
Therefore ![]() (Constant) = 0.
(Constant) = 0.
2) ![]() [c f(x)] = c
[c f(x)] = c ![]() (f(x)); where c is a constant why?
(f(x)); where c is a constant why?
Let g(x) = c.f(x)
Where c is constant and f(x), xÎR be a differential function of x. We then have,
![]()
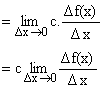
Thus ![]() [c f(x)] = c
[c f(x)] = c ![]() (f(x)).
(f(x)).