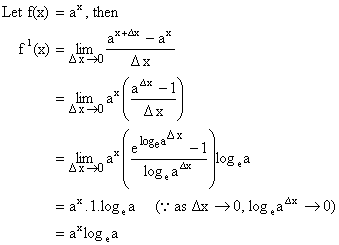differentiation-3

3)  Why?

Proof:

Let y = f₁(x) + f₂(x), Where f₁(x) and f₂(x) are differentiable functions of x.

Then

Thus .

4) Why?

Proof:

Let y = f₁(x).f₂(x) where both f₁(x) and f₂(x) are differentiable function of x.

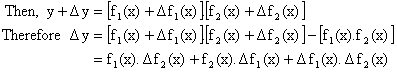
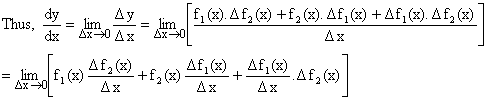
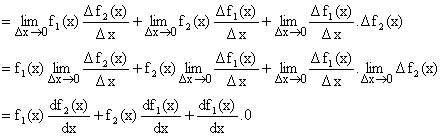
5) 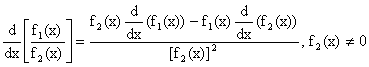 Why?

Proof:

Let , where f₁(x) and f₂(x) are differentiable functions at all points in its domain and f₂(x) ¹ 0.

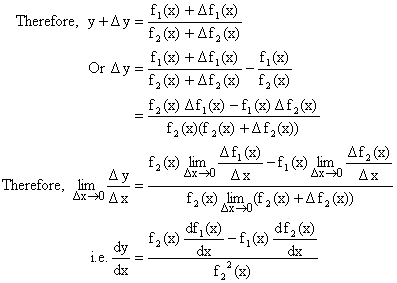
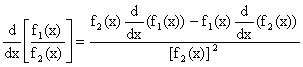
6) Why?

Proof:

Let y = f (t), t = g(x)

Then y = f (g(x)) is a function of x.

Dy = f (t+Dt) - f (t)

And Dt = g (x+Dx) - g(x)

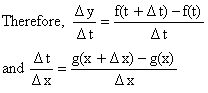
Assuming that for sufficient small values of Dx, Dt ¹ 0 this will necessarily be the case if then since g is differentiable it is continuous and hence when Dx®0, x+Dx®x any g(x+Dx) ® g(x).

Therefore t+Dt®t and Dt®0, since Dt ¹ 0 and Dx®0 we may write,

.

Clearly f and g are both continuous functions because they are differentiable thus Dt®0 when Dx®0 and Dy®0 when Dt®0.

Hence

Standard Formulae of Differentiation:

1)

Proof:

Let

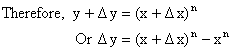
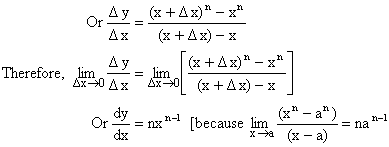
Thus

2)

Proof:

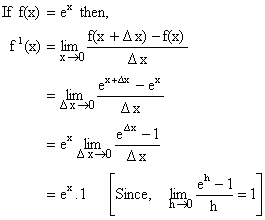
Thus

3)

Proof:

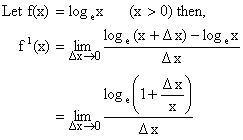
So,

4)

Proof: