differentiation-4

5)

Proof:

Let f(x) = sinx then,

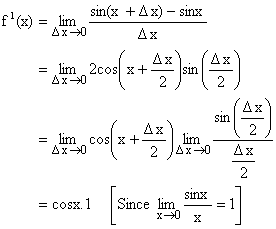
Hence,

6)

7)

8)

9)

10)  Why?

Proof:

Let f(x) = secx

Hence,

11)

Proof:

Let  then x = siny.

Differentiating w.r.t x we get,

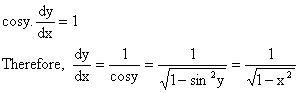
Hence,

12)

13)

14)

15)

16) Why?

Proof:

Let y = sec^-1x then secy = x.

Differentiating w.r.t x we have,

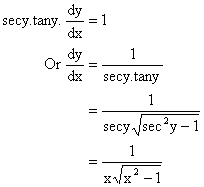
Hence,

Dumb Question:

Why and not ?

Ans:

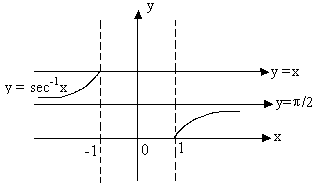
     Fig (4)

Note that y = sec^-1x is an increasing function in its domain.

So,

Illustration 6:

Differentiate

Solution:

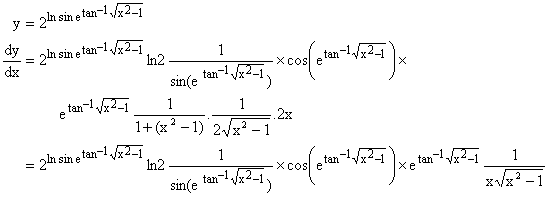
Different Methods of Differentiation:

1) Differentiation of a function defined parametrically:

Let x, y be function of parameter t, i.e.

x = f (t), y = f (t) then,

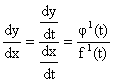
Illustration:

Solution:

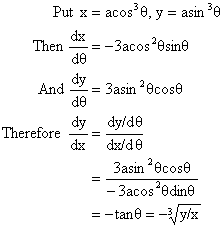
2) Logarithmic Differentiation:

The process of taking logarithm on both sides and then differentiating is called logarithmic differentiation.

Illustration 8:

Differentiate w.r.t x.

Solution:

Let y = .

Taking logarithm on both sides, then we have

logy = sinx.logx

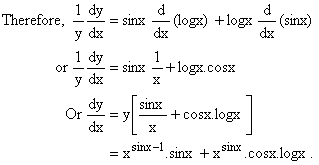
3) Differentiation of Implicit function:

If the relation between x and y is given by equation containing both and this equation is not immediately solvable for y, then y is called implicit function of x.

Illustration 9:

If  Then prove that

Solution:

Given that  differentiating on both sides w.r.t x we have,

Hence,