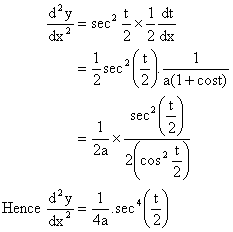differentiation-5
4) Differentiation of a function w.r.t other functions:
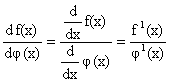
Illustration:
1) Differentiate 
with respect to tan-1x.
Solution:
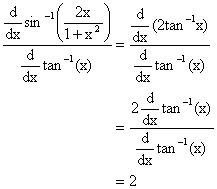
2) Differentiate ln tanx with respect to 
Solution:
5) Higher Order derivatives:
Let y = f(x) be differentiable function such that z = f1(x) is also differentiable. Then second derivative of y = f(x) is denoted by 
and 
.
In general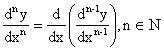 
Illustration 11:
For the curve 
find the rate of change of slope at (4, 27).
Solution:
We know that slope of a curve is given by 
. Now let g(x) denote slope of curve.
So, 
Now rate of change of slope = 
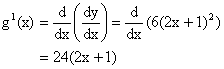
So rate of change of slope at (4, 27)
= 24(2´4+1)
= 216.
DIFFERENTIATION (EASY TYPE)
1) Differentiate 
with respect to x.
Solution:
Let y = then,
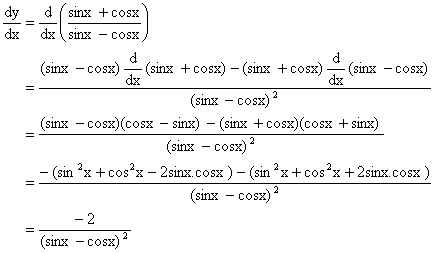
2) Let f be twice differentiable such that f11(x) = -f(x) and f1(x) = g(x). 
Where h (5) = 11, find h (10).
Solution:
Given 
on differentiating both sides w.r.t x we get
Now 
From (1) and (2) we get,
Therefore h1(x) = 0.
So, h(x) must be constant [as d/dx constant = 0]
But h (5) = 11 so h (x) = 11
Hence, h (10) = 11.
3) Find the sum of series 
using calculus.
Solution:
Let 
which is a geometric progression.
Therefore = 
On differentiating both sides, we get,
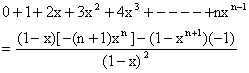
4) If 
and 
then find 
.
Solution:
Differentiating 
w.r.t x, we get,
5) If 
then find at 
.
Solution:
Putting t = cosq.
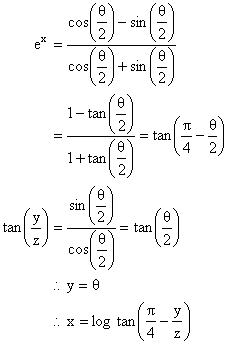
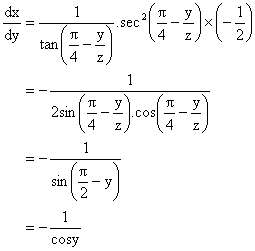
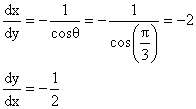
6) If 
a polynomial of degree 3 then find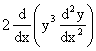 
in terms of P(x) and its derivative.
Solution:
We have 
And 
Also
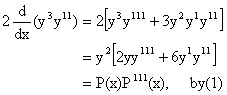
7) If 
Solution:
Taking log on both sides
ylogx + xlogy = log1.
Differentiating on both sides we get,
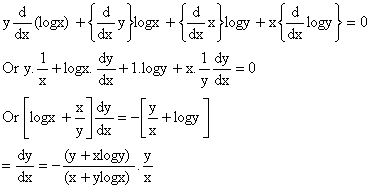
8) If x = a (t+sint) and y = a (1-cost), Then find 
Solution:
Here x = a (t+sint) and y = a (1-cost).
Differentiating both sides w.r.t t we get,
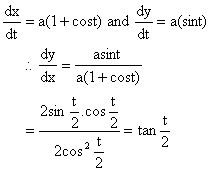
Again differentiating both sides we get,
