differentiation-7
3) Let f be differentiable function such that, 
find f(x)?
Solution:
Given that
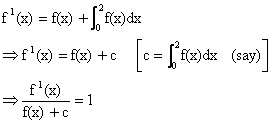
Integrating above expression both sides,
Where k is a constant of integration
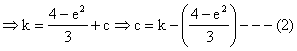
From (1) and (2) we get,
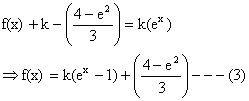
Now to find constant of integration k.
Integrating both sides from 0 to 2 we get,
Putting k=1 in (3) we get,
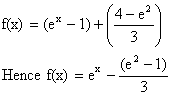
4) Let f(x+y) = f(x) –f (y) + 2xy -1 for all x, y ÎR, if f(x) is differentiable and 
prove that f(x)>0 for all xÎR.
Solution:
Putting x = 0 = y in given functional equation, we get f (0) = -1.
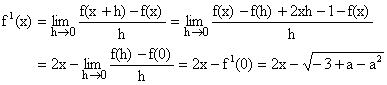
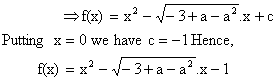
The discriminant
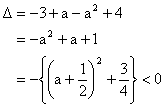
Hence, f(x) > 0 for all xÎR.
Dumb Question:
1) How does 
transform to 
?
Ans:
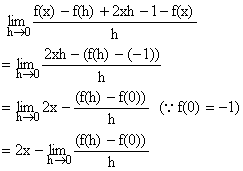
5) If 
then express y as an explicit function x and prove that 
.
Solution:
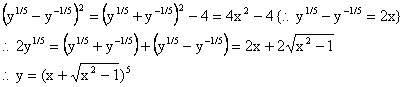
Differentiating w.r.t x,
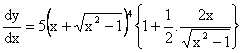
Differentiating w.r.t x,
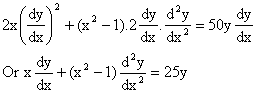
Therefore 
for then y is constant.
Dumb Question:
1) Why is 
?
Ans:
6) The function y = f(x) is defined as follows, x = 2t-|t|, y = t2 + t |t|, tÎR. Then discuss the continuity and differentiability of the function at x=0 also draw the graph of the function in the interval [-1, 1].
Solution:
When t < 0, x = 2t -(-t) = 3t < 0.
y = t2 + t (-t) = 0.
\y = 0 when x<0.
When t ³ 0, x = 2t-t = t ³ 0.
y = t2+t (t) = 2t2 = 2x2
\ y = 2x2 when x ³ 0.
Thus the function is as follows.
f (x) = 0, x<0
=2x2, x ³ 0
Now,
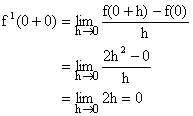
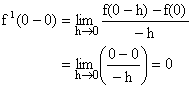
\f (x) is differentiable (finitely) at x=0.
\ f (x) is also continuous at x = 0.
Being a polynomial function f(x) is continuous at other points of the interval [-1, 1].
Now in the interval [-1, 1] we have y = 0 in [-1, 0], y = 2x2 in [0, 1]
So the graph is as below.
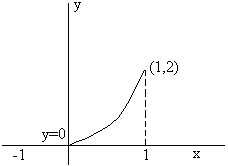
Fig (5)
(HARD TYPE)
1) 
Determine f {f(x)} and hence find the points of discontinuity and non-differentiability. Also draw the graph of f {f(x)} in [0, 3].
Solution:
Clearly f {f(x)} = 1+ f(x), 0 £ f(x) £ 2
3 - f(x), 2 < f(x) £ 3
When 0 £ f(x) £ 2
0 £ 1+x £ 2, if 0 £ x £ 2 {using first piece of definition}
Þ -1 £ x £ 1 if 0 £ x £ 2
Þ 0 £ x £ 1 (taking the interval of common points)
\ 0 £ f(x) £ 2 when 0 £ x £ 1 and f(x) = 1+x --------- (1)
When 0 £ f(x) £ 2
0 £ 3-x £ 2 If 2 < x £ 3 (using the second piece of definition)
Þ -3 £ -x £ -1 If 2 < x < £ 3
Þ 1 £ x £ 3 If 2 < x £ 3
Þ 2 < x £ 3 (taking interval of common points)
\0 £ f(x) £ 2 when 2 < x £ 3 and f(x) = 3-x ----- (2)
When 2 < f(x) £ 3
2<1+x £ 3 If 0 £ x £ 2 (using the first piece of definition)
Þ 1< x £ 2 If 0 £ x £ 2
Þ 1< x £ 2
\2< f(x) £ 3 when 1< x £ 2 and f(x) = 1+x ------- (3)
When 2< f(x) £ 3
2<3-x £ 3 If 2 < x £ 3 (using second piece of definition)
Þ -1 < -x £ 0 If 2 < x £ 3
Þ 0 £ x <1 If 2 < x £ 3
Þ xÎf.
Thus we get
f {f(x)} = 1+1+x = 2+x, 0 £ x £ 1 {from (1)}
= 1+3-x = 4-x, 2 < x £ 3 {from (2)}
= 3-(1+x) = 2-x, 1 < x £ 2 {from (3)}
Hence the function is
f {f(x)} = 2+x, 0 £ x£ 1
2-x, 1< x £ 2
4-x, 2 < x £ 3