As the polynomial functions are continuous and differentiable every where f {f(x)} is continuous and differentiable in [0, 3] except perhaps at the turning points of definition, namely, x = 1, 2 denote f {f(x)} by g(x).
Now g (1+0) = 2-1=1
g (1-0) = 2+1 = 3
So g(x) is not continuous at x=1.
g (2+0) = 4-2 =2
g (2-0) = 2-2 = 0
So, g(x) is not continuous at x=2.
Hence g(x) is also not differentiable at x = 1, 2.
\The points of discontinuity and non-differentiability are x=1, 2.
Now we have to draw the graph for y = f {f(x)} where
y = 2+x in [0, 1],
y = 2-x in [1, 2]
y = 4-x in [2, 3]
The graph is discontinuous at x = 1, 2.
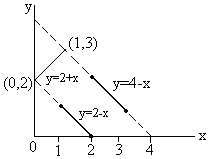
Fig (6)
Dumb Question:
1) In the above solution, there is a condition 0 £1+x £2 if 0 £ x £ 2 from that it is inferred that 0 £ x£ 1 How?
Ans:
0 £1+x £2 if 0 £ x £ 2
Þ -1 £ x £ 1 if 0 £ x £ 2
Now clearly both the conditions need to be satisfied simultaneously. So the intersection of these two conditions will give the desired results.
i.e. 0 £ x £ 1
2) If 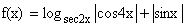 then find
then find  from the first principle.
from the first principle.
Solution:
Clearly the definition of the function f(x) is 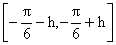 where h is a very small positive quantity, remains the same, so
where h is a very small positive quantity, remains the same, so 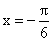 is not a turning point of definition.
is not a turning point of definition.
Now,
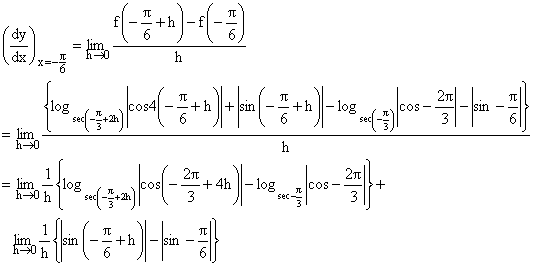

(Using definition of mod)

Now 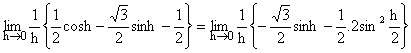
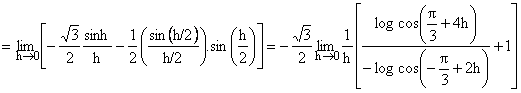

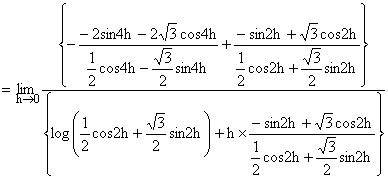
(Using L-Hospital Rule)
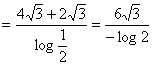

3) Let a+b =1, 2a2+2b2 =1 and f(x) be a continuous function such that f (2+x) +f(x) = 2 for all xÎ(0, 2) and p =  then find the least positive integral values of ‘a’ for which the equation ax22-bx+c = 0 has both roots lies between p and q;
then find the least positive integral values of ‘a’ for which the equation ax22-bx+c = 0 has both roots lies between p and q;
Where a, b, c ÎN.
Solution:
Given a+b =1 --------- (1)
2a2+2b2 =1 -------- (2)
Solving equation (1) and (2) we get,
a = b = 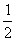 .
.
Þ  ----------- (3)
----------- (3)
Given f(x+2) +f(x) = 2 for all x Î[0, 2] -------- (4)
Now p = 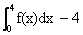

(let x = t+2 for second integration}

Then p =0, q=1
Let the roots of equation ax2-bx+c = 0 be a and b
\f (x) = ax2-bx+c= a(x-a) (x-b) -------- (5)
Since equation f(x) = 0 has both roots between 0 and 1.
\f (0).f (1) > 0 ------- (6)
But f (0).f (1) = c (a-b+c) = an integer ------- (7)
Therefore least value of f (0). f (1) = 1 -------- (8)
Now from equation (5)
f (0).f (1) = a a b a (1- a) (1-b)
= a2ab (1- a) (1- b) --------- (9)
As we know
a (1- a) has greatest values 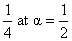 and b (1- b) has greatest value
and b (1- b) has greatest value 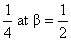
But b ¹ a
Thus from equation (8) greatest value of
f (0). f (1) <  ------ (10)
------ (10)
From (8) and (10)

{As a Î Natural number}
Dumb Question:
1) Why c (a-b+c) is an integer?
Ans: It is given in the question that a, b, c ÎN
So, cÎN and a-b+cÎI
So, c (a-b+c) ÎI
Hence c (a-b+c) is an integer.
KEYWORDS
ü Derivative
ü First Principle
ü 
ü Right Hand Derivative
ü Left Hand Derivative
ü Parametric
ü Logarithmic Differentiation
ü Implicit function
ü Chain Rule