Electric Current - 2

Illustration - 3. Find the current in brand BE and potential difference V_BD in.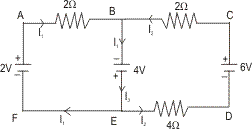



Assume the shown current distribution.
We can choose arbitarily any type of distribution as we like.
Applying kirchoff’s junction law at B (or at E).
We get : I₁ + I₂ = I₃ …………………………… (1)
Applying kirchof’s voltage law in the loop ABEFA: (clockwise direction)
We get :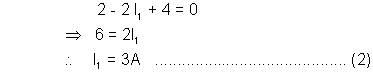

Applying kirchoff’s voltage law in BCDEB (Clockwise direction)
We get :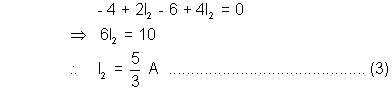

on solving (1), (2) and (3) :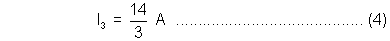

For potential drop across V_BD :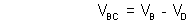

Let us search from B to D via C :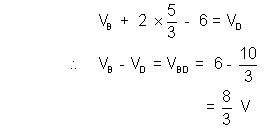


Question :-
route which connects B and D. It is recommended to go via shortest possible route to avoid long calculations and maping problem more complex.

Internal resistance of a battery
The potential difference across a real source in a circuit is not equal to the e.m.f of the cell,

Dumb question :- Why this happens ?

Solution :- The reason is that charge moving through the electrolyte of the cell encounters same resistance known as, internal resistance of the cell.

It is denoted by r. so, there is a potential drop across the ends of the e.m.f source.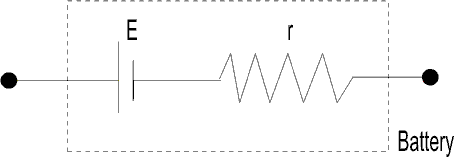



Potential difference (V) across the terminals of a battery -
For an e.m.f source, the potential changes will be obtained as illustrated below :-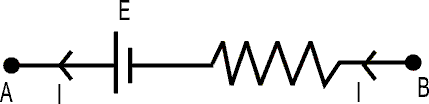





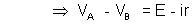
Special Cases :-

1. It current flows in opposite direction then,
   V = E + ir
   
2. V = E if current through the cell is zero.
   
3. V = 0 if the cell is short circuited.
   
   Dumb question - 8.
   Why V = 0 if the cell is short circuited ?
   
   Ans :-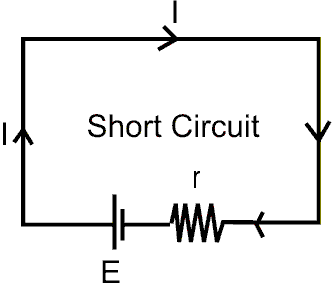
   
   
   NOw in this case applying kirchoff’s voltage loop law,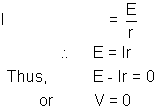
   
   
   Ilustration - In the given circuit
   E₁ = 10 V, E₂ = 8 V, r₁ = r₂ = 2.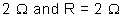
   
   
   
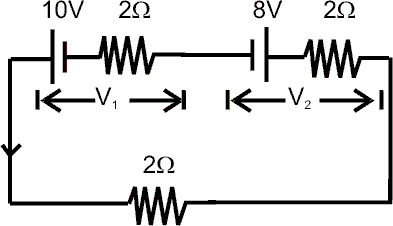
   Applying kirchoff’s voltage law in the circuit (moving anticlockwise)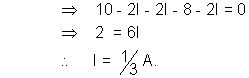
   
   
   
   
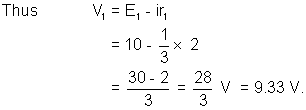
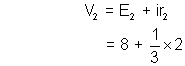
   Gruping of Resistances :
   
4. In series : R_eq = R₁ + R₂ + R₃ + …………………. R_n
   Equivalent resistance is defined as :
   
   where V = Voltage of battery
   I = Current following through battery.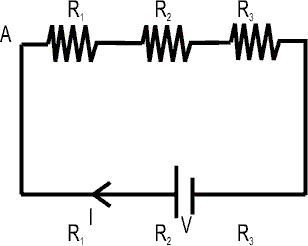
   
   
   
   Using kirchoff’s loop rule in clockwise direction we get: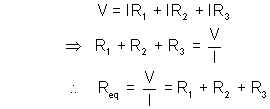
   
   Thus, R_eq across AB = R₁ + R₂ + R₃ further if battery has any internal resistance it will be added to give total resistance.
   
   
5. In parallel R_eq = R₁ + R₂ + R ₃ + ……….. + R_n
   Here also,
   Suppose, in the given figure we have to find R_eq across AB :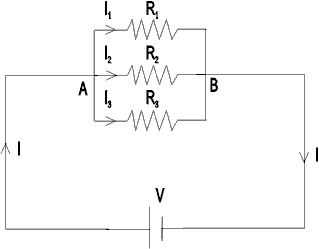
   
   
   Assuming the following distribution of current as shown.
   Applying kirchiff’s Junction Law at A.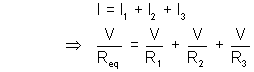
   
   (Because potential drop across each are same being in parrallel.)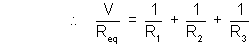
   
   
   
   
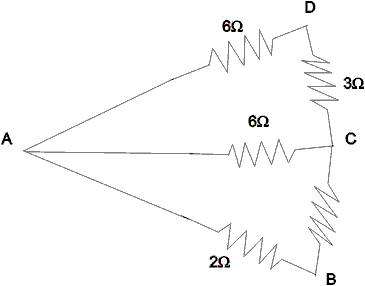
   Ans:- Resistance AB and BC are in series.