Electric Current - 4
(b) Parallel grouping :-
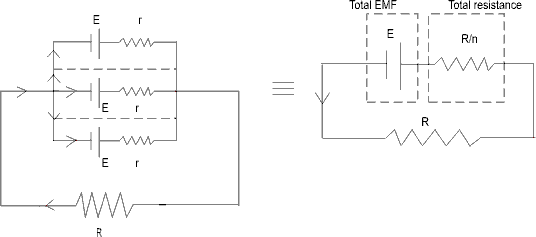
Applying Kirchoff’s Law through branch :
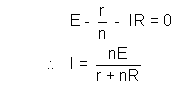
(c) Series grouping with different batteries :-
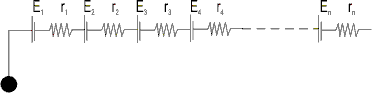
Eeq = E1 + E2 + E3 +……………….. + En
Req = r1 + r2 + ……………………………. + rn
(d) Parellel Grouping with different batteries :-
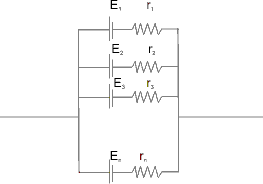
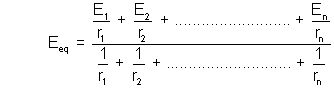
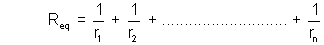
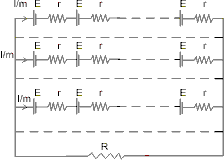
Number of rows are m and numbers of cells - in each rows in n :-
So, it is equivalent -
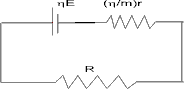
Applying Kirchoff’s laws :-
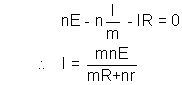
Dumb question :- How is total emf mE ?
Solution :- ’m' . ‘E’ rated batteries are in series so net emf becomes mE.
Dumb Question :- How is net resistance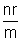 
?
Solution :- ’m' batteries in each row means ‘mr’ resistance becomes .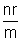
Illustration - 8. Find the equivalent emf and resistance of a single battery which is equivalent to a combination of al these batteries in the figure.
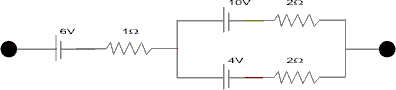
Ans :- For parallel combination :-
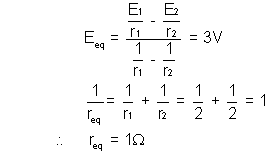
Now, this is in series with 6V battery -
Thus, net e.m.f. = (6 -3)V
And internal resistance = 2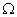
So, the equivalent circuit is -
a) Galvanometer :- It can detect very small currents as it has negligible resistance.
The corresponding potential difference for full scale deflection is :-
V = ig.G
b) Ammeter :-
IT IS ALWAYS CONNECTED IN SERIES WITH THE BRANCH ‘I’ HAS TO BE MEASURED !
It is a corrent measuring instrument. A galvanometer can be converted into a ammeter by connecting a small resistance S (called shunt) in parallel with it.
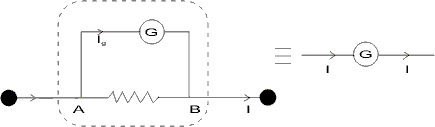
Thus, S(I - Ig) = G X Ig
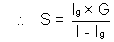
Dumb Questions :- Why is S in parallel ?
<>Solution :- As S is in parallel the current (I - Ig) will be very high while Ig will be lo. So that the potential difference VA - VB does not change much.
Dumb Questions :- Why is Ig ?
<>Ans :- Ig is that current which gives full scale deflection in galvanometer.
TO THE BRANCH WHOSE BE MEASURED !
A voltage measuring device is called a voltmeter. It measures the potential difference between two points. A galvanometer can be connecting a high resistance (R) in series with it.
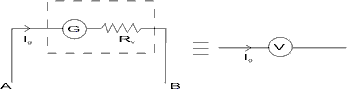
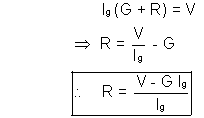
Dumb Questions :- Why is RV high ?
Solution :- If a large register (RV) is applied in parallel to two points then it doesn’t draw any current as RV is high. So Ig is very low. And hence the current IAB doesn’t change much.
Dumb Questions :- What is the ideal resistance for as ideal ammeter and ideal voltmeter ?
Ans :- For ideal ammeter R = 0
For ideal voltmeter R =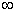 
Illustration - 9. A galvanometer having a coil resistance of 50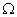 gives a full scale deflection when a current of 0.5mA is passed through it. What is the value of the resistance which can convert this galvanometer into ammeter giving full scale deflection for a current of SA ?
Ans :- As we derived earlier :
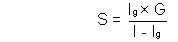
Now, Ig = .5 
10- 3A.
I = 5 A.
G = 50
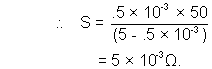
As expected it is coming out to be very low.
In ideal ammeters this shunt resistance is 0.
Illustration - 10 :- How can we make a galvanometer with G = 20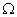
and Ig = 1mA in to a voltmeter with a maximum range of ISV ?
Ans :- Using
.
we have,
.
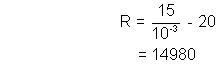As expected it is very high.
In ideal voltmeter it tends to infinity.
* Tip :- The basic Aim of using such devices is that they don’t affect the current much when used. And hence the voltmeter is such that when it is used, it doesn’t draw much current so that potential difference remains the same and is such that it also doesn’t let the voltage to da between the two points where it is installed. (and hence doesn’t change the current).
WHEATSTONE’S BRIDGE
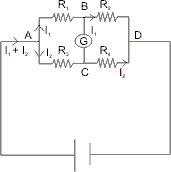
In this system suppose galvanometer shows null (zero current.
Then VBC = 0
VB - VC = 0
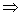VB = VC
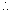I1R1 = I2R3 …………………………………… (1)
Similarly form other ends
I1R1 = I2R4 …………………………………… (2)
Dividing (1) and (2) :
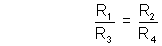
And, At this point the bridge is said to be balanced.
Dumb Questions - 14. Why on value of current through galvanometer to be zero VBC = 0 ?
Ans :- Current flows between two points only if there is any potential difference between those points. Here, in this case as current through BC is zero, this suggests that potential of B equals the potential of C. Hence VB = VC or VB - VC = 0 or, in other words VBC = 0.
So if between B and C, another resistance is placed, then no current flows through that resistance.