Electric Current - 5 · KnowledgeBin.org

d) Potentiometer :-
It is a device used to measure potential difference with high accuracy, without drawing any current from the unknown source. [* Basic Figure of a potentiometer : ??]
Principle of Potentiometer
It is based on the principle, that a current carrying wire has potential difference across its ends proportional to its length with a uniform cross sectional area.

It can be used for various purpose :

(1) To find e.m.f. of an unknown battery :
First a known battery (E_k) is placed as :

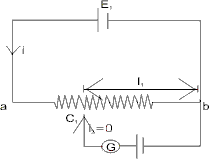
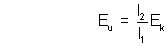
Suppose the null point is at l₁
Then, E_k = i(l l₁) ………………………………………(1)

Dumb Questions - 15. What is this null point ?

Ans :- On a close observation we can see that potentiometer is similar to wheatston’s bridge.
At null point current through galvanometer equals 0.
Now, the known battery is replaced by unknown battery (E_u).

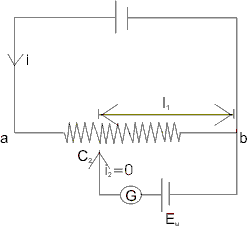
Now, E_u = I(l l₂) ………………………………………. (2)
From (1) and (2)

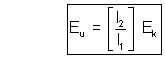
2. Find internal resistance(r) of an unknown battery.
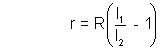, where R is a known resistance.
For any circuit for battery : V = E -ir = iR
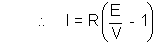………………………………….. (A)
Where R = external resistance.
r = internal resistance.
We connect a battery of e.m.f. E and internal resistance r as:

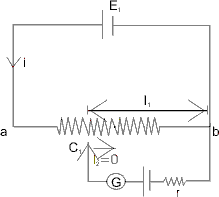
Now, E = ill₁ …………………………………………. (1) Now a known resistance R is connect across the terminals as :

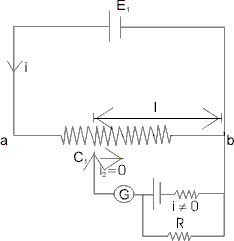
Now,
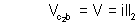……………………………………… (2)
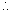from (1) and (2)
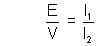……………………………………… (3)
Now, placing value of (3) in (A) :

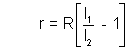
Question :- Find current in all branches

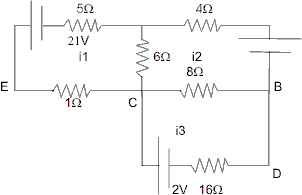
Ans :- Assume the current distribution as shown :
Applying kirchoff’s loop law in the three loops we get :
2l - Si₁ - 6(i₁ + i₂) - i₁ = 0 ………………………………….. (1)
S - 4i₂ - 6(i₁ + i₂) - 8(i₁ + i₃) = 0 …………………………..(2)
2 - P(i₂ + i₃) - 16i₃ = 0 ……………………………………… (3)
On simultaneously solving there three equations we get :

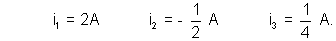
Dumb Question - 16. In branch AC which will we Lonsides i₁, i₂ ?

Ans :- We will Lonsides the current i₁ + i₂ in AC as we have Lonsidered that in those two loops different currents i₁ and i₂ are flowing now, their common edge will have the sum according to the direction of two currents. This is called principle of superposition.

E2 :- Two resistance have temprature coefficient 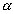₁ and 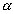₂ and R₀₁ an R₀₂ the resistance at 0⁰C. Find 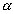_eq if they both are connect (a) in series and (b) in parallel ?

Ans :- For series :
At 0₀C R_eq = R₀₁ + R₀₂ ………………………………………… (1)
At any temperature t₀C
R_eq = R₀₁ + R₀₂
R_eq = R₀₁[1 + 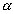₁(t - 0)] + R₀₂[1 + 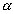₂(t - 0)]
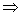[R₀₁ + R₀₂][1 + 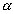_eqt] = R₀₁[1 + 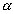₁t] + R₀₂[1 + 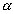₂t]

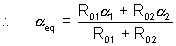
In Parallel :
At t₀C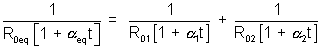
Using Binomial Expansion :

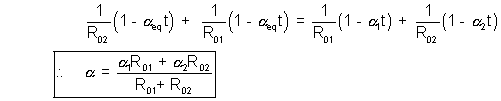
E3. A rod length L and cross sectional area A lies along the axis between x = 0 and x = L.

Its resistivity is given by : P(x) = P₀.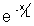
The end x = 0 is at a potential V₀ and x = L at V = 0.
(a) Find net resis tance of the rod.
(b) The electric potential V (n) ?

Ans :- (a)

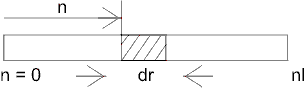
At any distance n suppose an elementary particle dn be considered such that dn 0.
Its resistance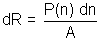
As R =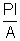

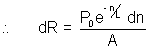
Thus, R =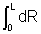

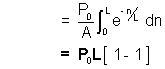
(b) We know that,
Potential difference = i dR = dV

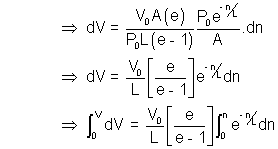
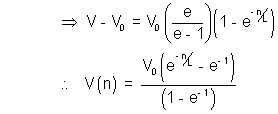
04. A battery of e.m.f. 1.4V and internal resistance 2 is connected to a 100 resistor through an ammeter. The resistance of te ammeter is .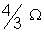
If ammeter rods .02 A. What is the resistance of the Voltmeter ?

Ans :- Circuit diagram is :

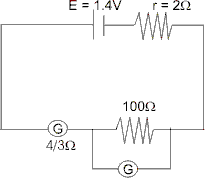
Now first finding total resistance of the circuit.

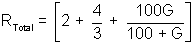
where G = Resistance of voltmeter.
Now, Current =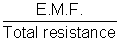

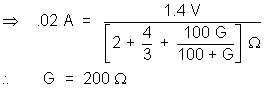
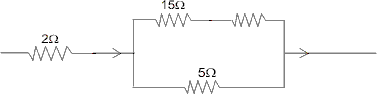
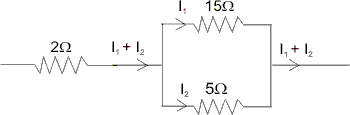
In the given circuit 5 resistor develops 45 J/s Power due to current flowing through it. Calculate the heat developed/second through 2 resistor ?

Ans :- Assume the shown current distribution after writing equivalent circuit :

Related Guides