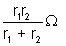Electric Current - 6

Now, as power through 5 resistance is 45 J/S.

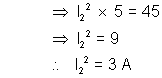
Applying Kirchoff’s loop rule in the loop.

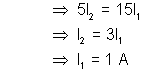
Thus, net current is 4A through 2 resistor.
Thus, power lost from this resistance = (2) X 4₂ = 32 J/S.

Question :-
Connected is series and have different internal resistances r₁ and r₂( >l₁). Find an external resistance R at which the potential difference across the terminals of one of the sources becomes equal to D ?

Ans :- V = E - ir E and i for both the sources are equal. Therefore, potential difference V will be zero for a source having greater internal resistance, that is, r₂.

.

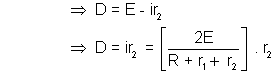
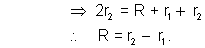1. Six equal resistances of 4 each are connect as shown. Find R_eq about PQ.
   
   
   
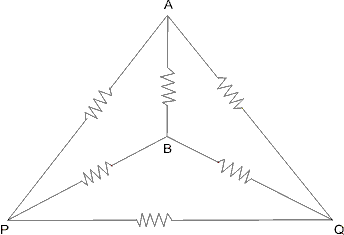
   Ans :- Finding R_eq about PQ.
   The Circuit is equivalent to :
   
   
   
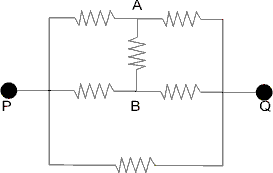
   Now, current through AB is zero, as it is a balanced Wheat Reduces Stone Bridge.
   Thus, the circuit reduces to
   
   
   
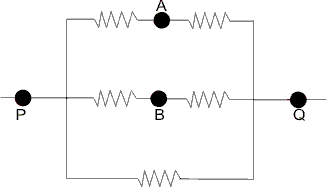
   Thus,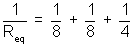
   .
   
   
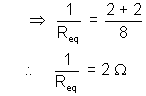2. Find the potential difference V_a - V_b in the circuit shown in the figure :
   
   
   
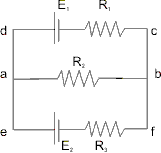
   Ans :- Assume the shown current distribution :
   
   
   
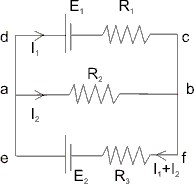
   Applying kirchoff’s voltage law in abcda :
   E₁ + I₁R₁ = I₂R₃ …………………………….(1)
   
   Applying kirchoff’s voltage law in abfca :
   I₂R₃ + (I₁ + I₂)R₂ = E₂ ……………………………(2)
   
   Using (1) and (2):
   
   
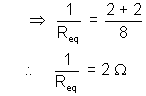
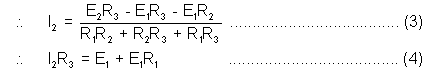
   Thus, V_a - V_b = I₂R₃
   
   
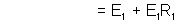
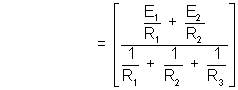   [Using (3) and (4)]
   
   Question :-
   
   
   
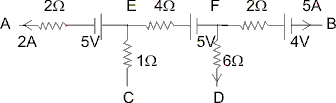
   Certain circuit :
   Find
   (a) Power dessipated in 6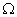 resistance.
   (b) V_C - V_B.
   
   (c) V_A - V_D ?
   
   Ans :- (a) Power in 6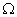 = I²R
   
   
   (b) Now, Applying Kirchoff’s Voltage law at E.
   Current through 1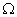 resistor = 9A.
   .
   
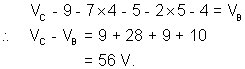   (c) V_D - 12 + 5 + 28 - 8 - 4 = V_A
   
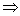   V_D - V_A = - 33V
   
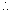   V_A - V_D = 33V
   
   
   M2: Find equivalent battery having same e.m.f. and equivalent resistance of a battery equivalent to V1 and V2 having internal resistances r1 and r2 in the adjoining figure .
   
   
   
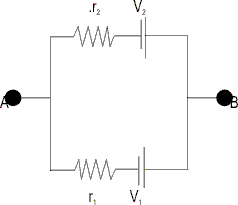
   Ans (1) Potential difference across the terminals of the battery is equal to e.m.f. when current drawn from the battery is zero. Assuming no current is coming out.
   So, Current distribution is :
   
   
   
   
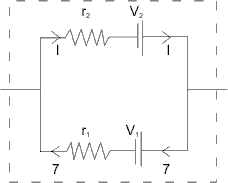
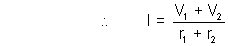
   Thus, V_A - V_B = Net equivalent E.M.F. = V₁ - ir₁(V₂ - ir₁)
   
   
   
   (2) As r₁ and r₂ are in parrallel.
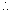   Equivalent internal resistance = r =