Electromagnetic Induction - 4
R - L Circuit:
Growth of current in an inductor:
Let us consider a circuit with battery of e.m.f. E, a coil L and a resistance R, as shown:
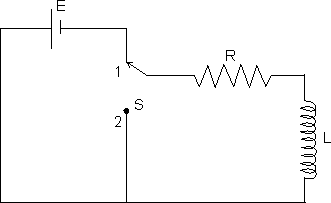
I = I0[1 -
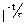 ]
]where
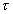 = L/R
= L/RWhen current is allowd through an inductor the growing current induces an opposite e.m.f. which opposes the growth of the current.
At position of swith,
- IR -
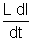 + E = 0
+ E = 0On solvingg this differential equation:
I =
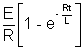
= I0[1 -
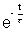 ]
]where
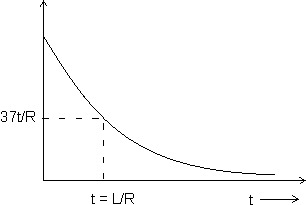
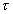 = Time constant = L/R.
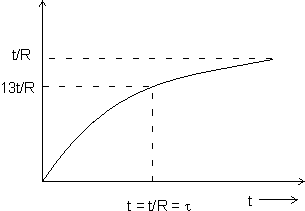
= Time constant = L/R.Dumb Question: What is the significance of time constant with respect to attainment of steady state ?
Ans: It measures the sapidity with which the final state as the steady state is approached and may be defined as the time in which steady state would have been reached if the current were allowed to increase at the initial rate.
Decay of current in an inductor:
In the same circuit if the switch 1 is shifted to switch 2, then the current decays in the inductor.
I = I0
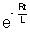
we have, -
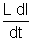 - IR = 0
- IR = 0on solving I = I0[
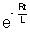 ]
]where I0 = current at time t = 0
ENERGY STORED IN AN INDUCTOR:
During the decay the energy needed to maintain the current is provided by energy stored in the magnetic field. LI =
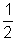 LI2
LI2Thus, the rate at which energy is dissipated in the resistor = rate at which the stored energy dereases in magnetic field of inductor.
or, I2R = -
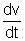
=> I2R = -

=> I2R = - LI[
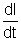 ]
] I2R = - LI[
I2R = - LI[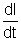 ]
]Illustration: A coil of resistance 20
 and inductance .5 H is switched to 200 V supply.
and inductance .5 H is switched to 200 V supply.Calculate the rate of increase of current:
(a) At the instant of closing the switch, and
(b) After one time constant.
(c) Find the steady state current in the circuit ?
Ans: (a) As I = I0(1 -
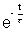 )
)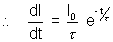
At t = 0
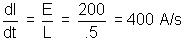
(b) Similarly at t =
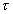
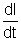 = 400 e-1 = .37 x 400 = 148 A/s.
= 400 e-1 = .37 x 400 = 148 A/s.(c) The steady state current in the circuit,
I0 =
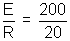 = 10 A
= 10 AL.C. Oscillations:
A capacitor is charged to a p. of V0 by connecting it across a battery and then is alowed to discharge through a pure inductor of inductance L.
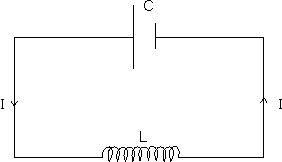
At any instant, let the charge on the capacitor be q and current in the circuit be I.
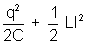 = constant ............................................... (1)
= constant ............................................... (1)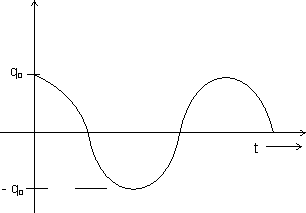
Differentiating w.r.t. time we get
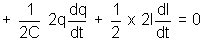
or,
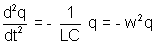 (where w = 2
(where w = 2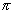 f)
f)which gives f =
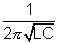
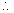 Current I in the circuit and the charge q on the plates of the capacitor vary sinusoidally as:
Current I in the circuit and the charge q on the plates of the capacitor vary sinusoidally as:I = I0 sinwt
q = q0 coswt
(If initially capacitor is charged to go)
But if, capacitor is uncharged and indutor is having a current I0 then:
I = I0 coswt
q = q0 sinwt
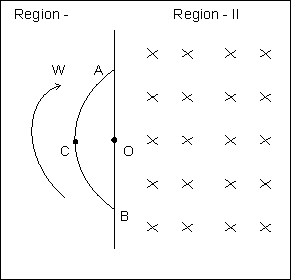
E1. A smicircular loop AOBCA having radius "r" and an effective rasistance "R" rotates between Region I and Region II with constant w a shown.
(a) Obtain an expression for the magnitude of induced current in the loop!
(b) Show the direction of the current when the loop is entering into the Region II.
(c) Plot a graph between induced e.m.f. and time of rotation for periods of rotation ?
Ans: (a)
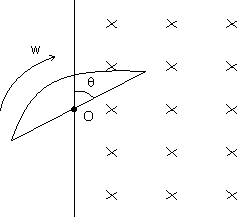
A =
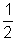 r2
r2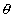
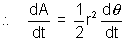
E = -
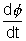
= - B
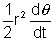 [
[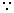
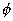 = BA]
= BA]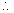 E = -
E = - 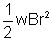 [as
[as 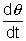 = w]
= w]