Electromagnetic Induction - 5
(b) The current is anticlockwise in the loop as it enters:
(c)
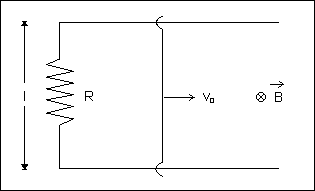
E2. A connecting rod AB of mass m slides without friction over two long conducting rails separated by a distance l.
Initially, the rod is moving with a velocity v0 to the right, find:
(a) The distance covered by the rod until it comes to rest.
(b) The amount of heat generated in the resistance r during the process ?
Ans: (a) Et =Blvt
It =
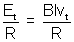
F (retarding) = ItlB =
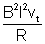
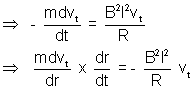
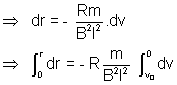
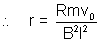
(b) Heat generated in resistance R = Loss in Kinetic Energy
=
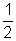 mv02 -
mv02 - 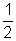 m(o)
m(o)=
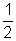 mv02
mv02E3. A small square loop of wire of side l is placed inside a large square loop of wire of side (L >> l). The loops are .... and their centres coincide. What is the mutual inductance of the system
Ans:
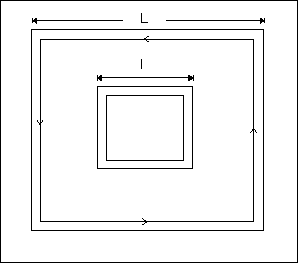
Consider the square loop th be made up of four rods each of length L, the field at the centre, that is, at a distance
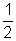 from each rod will be
from each rod will beB = 4 x
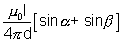
or, B =
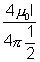 = 2 sin450
= 2 sin450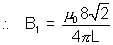 I
ISo, the flux linked with smaller loop:
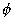 2 = B1S2 =
2 = B1S2 = 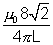 l2I and hence,
l2I and hence,M =
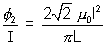
E4. What inductance would be needed to store 1 kwh of energy in a coil carrying a 200 A current ? (1 kwh = 3.6 x 106 J)
Ans: We have I = 200 A
U = 1 kwh = 3.6 x 106 J
Now, L =
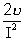 [As
[As 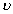 =
= 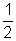 LI2]
LI2]=> L =
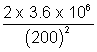
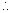 L = 180 H
L = 180 HE5. (a) Calculate the inductance of an air core solenoid containing 300 turns if the length of the solenoid is 25 m and its cross sectional area is 4 cm2 ?
(b) Calculate the self induced e.m.f. in the solenoid if the current through it is decreasing at the rate of 50 A/s.
Ans: (a) The inductance of solenoid is given by,
L =
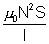
Substituting the values we have
L =
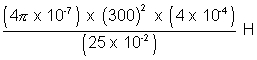
= 1.81 x 10-4 H.
(b) As t = -
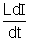
Here
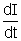 = - 50 A/s
= - 50 A/s=> E = - (1.81 x 10-4) x (- 50)
 E = 9.05 x 10-3 mv.
E = 9.05 x 10-3 mv.E6. A square wire frame with side a and a straight conductor carrying a constant current I are located in the figure. The inductance and the resistance of the frame are equal to L and R respectively. The frame was turned through 1800 about axis OO' which is located at a distance b from the current carrying conductor. Find the electric charge which passes through the frame.
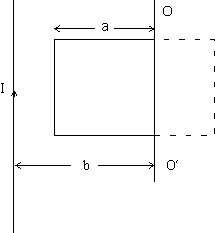
Ans: Electric charge through a loop =
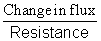
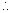 q =
q = 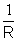 (
(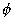 f -
f - 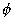 i)
i)Since d
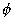 =
= 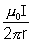 a dr
a dr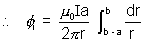
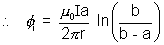 ; Similarly
; Similarly 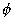 f =
f = 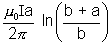
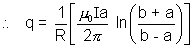
E7. A conducting square loop of side a
 is rotated in a uniform
is rotated in a uniform 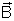 about P as shown in the figure. Find the induced e.m.f. between P and Q and indicate the relative polarity of points P and Q.
about P as shown in the figure. Find the induced e.m.f. between P and Q and indicate the relative polarity of points P and Q.
Ans: The rotation of the ring about point P generates an e.m.f. The ring within P and Q is equivalent to a rod of length PQ.
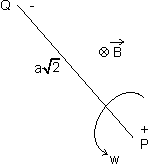
Now, PQ = a
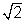
As we know that the e.m.f. across a rod of length l rotating with velocity w is =
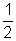 Bwl2
Bwl2Then e.m.f. between P and Q is given by:
t =
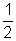 Bw(a
Bw(a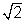 )2
)2 t = Bwa2
t = Bwa2