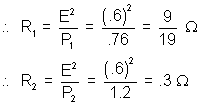Electromagnetic Induction - 6

E8. An inductor of inductance 2mH is connected across a charged capacitor of S_µF. Let q denote the instantaneous charge on the capacitor, and I the current in the circuit. Maximum value of Q = 200 µC.

(a) When q = 100 µC, what is the value of |dI/dt| ?

(b) When q = 200 µC, what is the value of I ?

Ans: (a) The expression for q is q = Q coswt
where w = 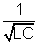= 10⁴ Hz
Now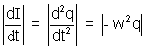   
(As in S.H.M.)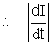
= 10⁸ x 100 x 10^-6 = 10⁴ A/s.

(b) When the energy of capacitor is maximum the energy stored in the inductor will be zero.
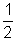   => LI² = 0

I = 0

M1. In the circuit diagram shown in figure R = 10 , L = 5 H, E = 20 V, I = 2 A. This current is decreasing at a rate of - 1 A/s. Find V_ab at this instant ?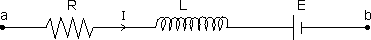


Ans: P.D. across inductor
         V_L =
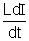
             = 5 x (- 1)
             = - 5 V
Now, V_a - IR - V₂ - E = V_b
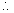     V_ab = V_a - V_b
             = E + IR + V_L
             = 20 + 2 x 10 - 5
             = 35 V


M2. A conducting rod of length l attached to a rod of insulating material of length L is rotated with constant anfular speed in a plane normal to uniform as shown.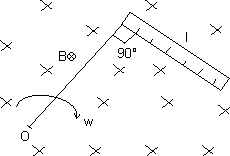


Find the e.m.f. produced across the ends of the conducting rod ?

Ans: Consider a small elemental length dn of the rod at a distance n from the end of the rod as shown.


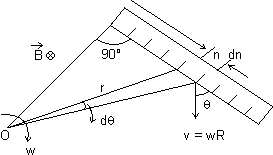
The e.m.f. across the elemental rod will be

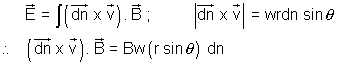
                  = Bwn dn

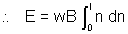
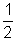      = wBl²

Note: The result is same as if the rod is rotated about one of its ends.


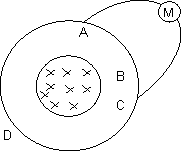
M3. A variable magentic field creater a constant e.m.f. E in a conductor ABCDA. The resistance of the portions ABC, CDA and AMC are R₁, R₂ and R₃ respectively. What current will be shown by meter M ?


The magnetic field is ...... near the axis of the circular conductor.

Ans: Let E₁ and E₂ be the e.m.f.s developed in ABC and CDA, respectively.
Then E = E₁ + E₂
There is no net e.m.f. in the loop AMCBA as it does not enclose the magnetic field. If E₃ is the e.m.f. in AMC then E₁ - E₃ = 0. The equivalent circuit and distribution of current is shown in figure:


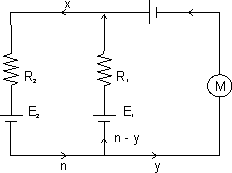
By loop rule:
      R₁(x - y) + R₂x = E₁ + E₂ = E

and R₃y - R₁(x - y) = E₃ - E₁ = 0

Solving for y



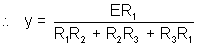
M4. Two parallel vertical metallic rails AB and CD re separated by 1 m. They are connected at the two ends by resistance R₁ and R₂ as shown in figure. A horizontal metallic bar of mass 2 kg slides without friction vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of .6 perpendicular to the plane of the rails. It is observed that when the terminal veloity is attained power dissipated in R₁ and R₂n are .76 w and 1.2 w respectively. Find the terminal celocity of the bar and the values of R₁ and R₂?


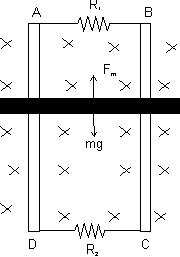
Ans: The rod will acquire terminal velocity only when magnetic force F_M = BlI due to electromagnetic induction balances its weight, that is:
    BIl = mg
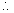I =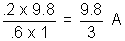
Now, if E is the e.m.f. induced in the rod,
     E x I = P = P₁ + P₂
So, E = 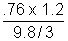= .6 V
Now as this E is generated due to motion of rod with terminal velocity in magnetic field:
    t = BV_Tl


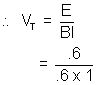
      = 1 m/s

Now, P =
    
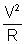
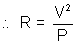
Here V₁ = V₂ = E