Electrostatic - 7
Now ![]() can be got easily by integrating, for it is independent of x, y, and z.
can be got easily by integrating, for it is independent of x, y, and z.
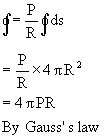
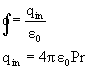
Note: The question although easy may seem very difficult during exam because of the use of Cartesian Co-ordinates. So student should go through the above example carefully.
Q-7: A non-Conducting disc of radius R and Surface charge density ![]() is placed on the ground with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of disc from height H with zero initial velocity. The particle has q/m= 4 e0g/
is placed on the ground with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of disc from height H with zero initial velocity. The particle has q/m= 4 e0g/![]()
a) Find value of H if the particle just reaches the disc.
b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
solution:
a) As proved earlier
Vi = potential on axis of a disc
![]()
Vf = potential at center ![]()
By conservation of energy:
Decrease in gravitational potential energy = Increase in electrostatic potential energy
KEi = KEf = 0 (As particle is at rest in both position)
mgH = q (Vf - Vi)
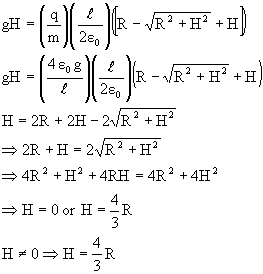
b) Net potential energy = electrostatic P.E + gravitational P.E
![]()
![]()
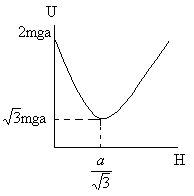
Fig (36)
Note:
1) Potential energy includes both electrostatic potential energy and gravitational potential energy.
Question:
1) How is K.E=0 in both position?
Ans: Initially it has zero initial velocity K.Ei=0, finally it is just able to reach the disc.
Final velocity = 0 Þ K.Ef =0.
Hard
Q-1: A non conducting sphere of radius R has a positive charge which is distributed over its volume with density ![]() per unit volume, where x is distance from the center. If dielectric constant material the sphere is K=1, Calculate energy stored in surrounding space and total self energy of the sphere.
per unit volume, where x is distance from the center. If dielectric constant material the sphere is K=1, Calculate energy stored in surrounding space and total self energy of the sphere.
solution: If strength of electric field at a point is E, energy stored per unit volume of dielectric at that point is ![]() hence to calculate density of electrostatic energy in surrounding space, first electric field strength is to be calculated. But for its calculation, total charge on sphere must be known.
hence to calculate density of electrostatic energy in surrounding space, first electric field strength is to be calculated. But for its calculation, total charge on sphere must be known.
Hence, first consider a thin spherical shell inside the sphere as shown in figure.
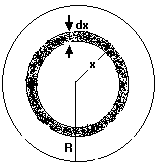
Fig (37)
Let radius of the shell be x and let radical thickness be dx.![]()
![]()
![]() Total charge on the shell is
Total charge on the shell is![]()
![]()
Now consider a concentric spherical shell (in surrounding space) of radius r (>R) and radical thickness dr.
Electric field at surface of this shell.
![]()
![]() Energy stored in the shell,
Energy stored in the shell,
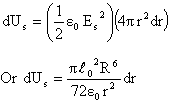
![]() Energy stored in surrounding space,
Energy stored in surrounding space,
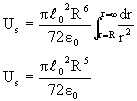
Self energy of the sphere is total electrostatic energy stored in surrounding space and inside the sphere.
To calculate energy stored inside the sphere, consider a concentric spherical shell of radius x and radical thickness dx. Electric field at surface of this shell is due to charge on inner concentric solid sphere of radius x.
Charge on this concentric sphere is
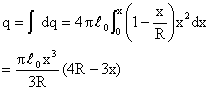
![]() Electric field at surface of this shell,
Electric field at surface of this shell,
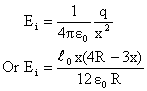
![]() Energy stored in the shell,
Energy stored in the shell,
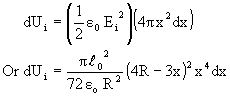
![]() Total energy inside the sphere is
Total energy inside the sphere is
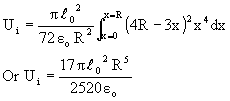
![]() Self energy of the sphere = Us+Ui
Self energy of the sphere = Us+Ui
![]()