Electrostatics - 2
Illustration:
Q-1: A field of 103 N/C acts at a point. What will be the force on a charge of 3´10-6C and -2´10-6C, kept there?
solution:
For +3MC
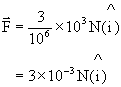
For -2MC
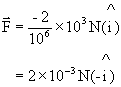
Discussion:
The direction of force changes for different charges. For a positive field (due to +ve charge)
1) The force is in direction of field on the +ve charge i.e. repulsive.
2) The force is opposite to field direction on the –ve charge i.e. attractive.
Similar inference can be drawn for negative charges.
Electric field due to:
a) Charged ring of charge Q and radius R.
1) The Center=0.
Derivation:
Linear charge density (l) on ring = 
Consider the field at center due to any element = 
But the field due to point diametrically opposite = 
in opposite direction.
\Net field at center = 0 (By symmetry)
2) On the axis =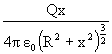 
On axis of ring at distance x.
Derivation:
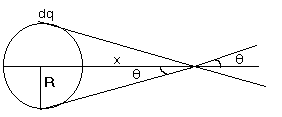
Fig (5)
As obvious from the diagram the field component along the line gets added due to opposite element.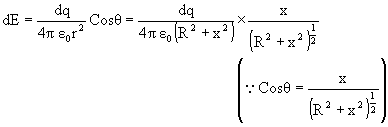
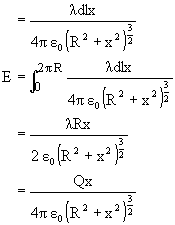
*) By substituting x=0 in 2nd result, we can get the first result.
*) Student should verify that the graph is of the following manner.
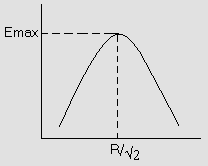
Fig (6)
b) Due to a straight charged rod of length 2L with charge per unit length ‘
’ at a distance ‘a’ on its perpendicular bisector.
E =
Derivation:
The rod is divided into infinitely small elements and the field due to symmetrically; opposite part add up as shown in figure (7).
Net field at P.
E = 
dE = 
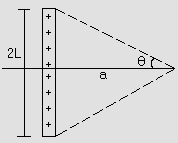
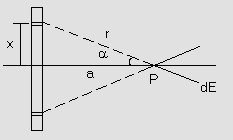
Fig (7)
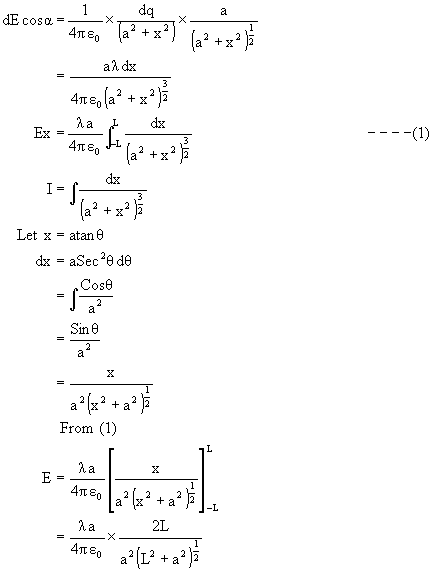
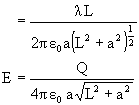
Useful Tips:
1) If x>>a, E = 
like a point charge.
2) If L
i.e. for infinite length
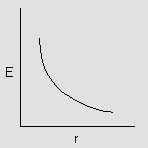
Question:
1) How did the electric field cancel in one direction and add in another?
Ans:
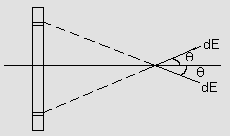
Observe the direction of electric field of two points which are symmetrically opposite.
Along the axis, net field = 
Along the perpendicular,
Net field = 
Similarly all fields along the perpendicular to axis cancel out.