Electrostatics - 3

Flux and Gauss Law:

Flux- It literally means the no of field lines passing through it. It is defined as.

 
Gauss law- The electric flux  through any closed surface is equal to  times the net charge enclosed by the surface.

               

Illustration:
A square frame of edge 5cm is placed such that a uniform electric field of 10 V/m makes 30⁰ with positive normal.

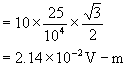
Application of gauss law:

1)   Uniformly charged sphere (solid) with charge Q and radius R.

       

        
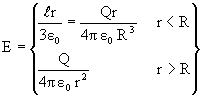
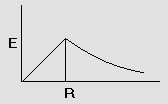
                Fig (9)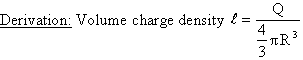

     
Case-1: (r>R)
                           
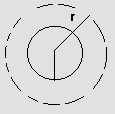
                                 Fig (10)

Charge enclosed = Q
     

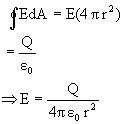
      Case-2: (r<R)

       

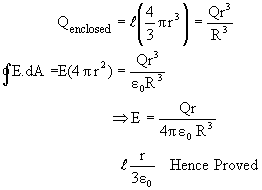
        Question:

            Q-1 How?

            Ans: The field lines should be radially outward and therefore collinear with outer normal.

Cos = 1

2)      Infinitely long linear charge distribution:

Derivation:
      Consider the Gaussian surface shown:

                                                     

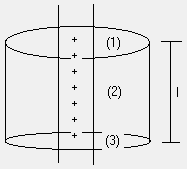
                                                                      Fig (11)

Q_enclosed = ll

For surface (1) and (3)

  

As electric field perpendicular to area vector for curved surface (2)

 

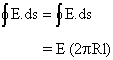
By Gauss’s law

E (2pRl) =

3) Field due to infinite charged plane sheet with charge density ()=

=

Derivation:

Consider a cylindrical Gaussian surface as shown.

Flux through curved surface = 0

                           

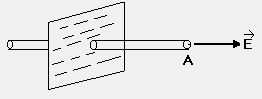
                                                  Fig (12)

 

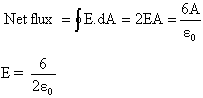
Conductors:
The electric field inside conductors is zero in electrostatic equilibrium.

Cavity in a conductor:
Consider the metallic shell with a post charge in the center.
Since E = 0 inside a conductor q _enclosed by G.S = 0
Þ -q charge is induced on inner surface, as shown in figure (13).
Since shell is neutral, +q is induced on outer surface as shown in figure (14).

             

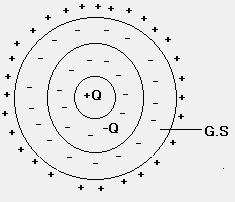
                Fig (13)                                                    Fig (14)

Question:
Explain why electric field inside a conductor is zero, with the help of induction.
Solution: A conductor has large no of free electrons. When it is kept in an electric field, electrostatic force acts on these electrons which draw most of the electron to one side causing negative charge on that side and positive charge on opposite side due to deficiency of electrons. The field due to these induced charges balances the external electric field and thus there is no electric field in the metal.

                    

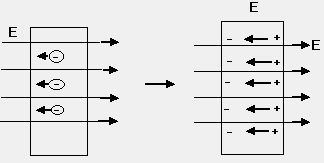
                                                     Fig (15)      

E_net =E+E_in = 0

On the surface of charged Conductor:

Electric field means a Conductor =

Force per unit area or electrostatic pressure experienced by a charged conductor =

(The derivation of above formula is not very important for IIT JEE preparation)

Energy density of electric field =