Electrostatics - 4

Electric Potential:
It is the work needed to bring a unit positive charge from infinity to the given point.

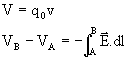    (Because, since the field is conservative.)

Q-1: The value of integral depends only on end points A and B why?

Ans:

 (As it is opposite to electrostatic force)

   

Note:

1)      It is a scalar quantity and has units Joules per coulomb (J/C) called Volt.

2)      Potential difference between two points A and B is V_B-V_A =

Where W_AB is work done in moving from A to B.

Electric potential due to a point charge =

Principle of superposition:

Net potential due to a system of charge is, V = V₁+V₂+V₃+V₄+----------------
In Cartesian Co-ordinate-

Illustration:
1)  Three charges q₁, q₂, q₃ are placed at (r, 0, 0), (0, 3r, 0), (0, 0, 2r) respectively. Find potential at origin.
Ans:

Net electric potential = Vq₁+Vq₂+Vq₃

                                        =

                                        =

Equipotential surface:

If a surface is drawn in such a way that electric potential is same at all points of the surface it is called equipotential surface.

    

• Work done in moving a charge on equipotential surface = 0.

Electric potential on –

  

Derivation:

      Divide the ring into infinite elements and potential due to each element.

                                          
                                                      Fig (16)

If r = 0, V at center =  as shown in figure (17)       

                                     

                                                           Fig (17)

2)      axis of uniformly charged disc =

Derivation: Consider disc having uniform surface charge 6(c/m²)                                    

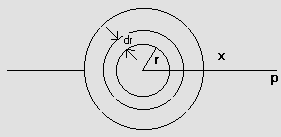
                                                               Fig (18)  

Potential due to ring of radius r =

 

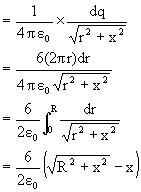
Question:

   Q-1:  How dq =

   Ans:  dq = 6 x Surface area

        =

 2r.dr= area of the ring.  

3)      Due to a Shell: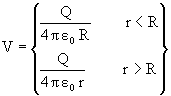

Derivation: Shell of radius R has charge Q

Case-1: (r>R)

     

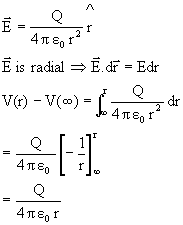
Case-2: (r<R)

E_inside = 0

 

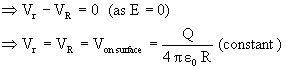
Electric Potential Energy:

1)      Potential energy between two charges q₁ and q₂ separated by distance r = .
2)    P.E due to System of charge =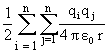

Change should be replaced with sign.

 

Question:

Q-1: Why ½ in the above expression?
Ans: If ½ were not produced each pair would be counted twice. For example- For q₁ and q₂

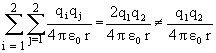
3)     

Illustration:
Two point charges are located on x-axis q₁= 3microcoulomb at x=0 and q₂= -1 microcoulomb at x=2m.
a)      Find work to be done to bring q₃= 1microcoulomb from infinity to x= 1m.
b)      Find total P.E of the system.

solution: Work done = difference in P.E.
= U_f-Ui

 

 

Earthing: Potential of earth is zero. If a conductor is earthed its potential becomes zero.

Tips for Concentric conducting spherical shells:
1)      Net charge inside a closed Gaussian surface drawn in any shell is zero.
2)      Potential of the earthed conductor is zero.
3)      Two connected conductors are at same potential.
4)      Charge remains constant in all conductors except those which are earthed.
5)      Charge on inner surface of innermost shell = 0 (if no charge is kept inside)
         Charge on outer surface of outermost shell = total charge enclosed.
6)      Equal and opposite charge appear on opposite faces.

Illustration:
Figure (19) shows two conducting thin concentric shells of radii r and 3r. The outer shell carries charge q. Inner shell is neutral. Find the charge that will flow from inner shell to earth after the switch S is closed.

                                       

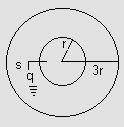
                                             Fig (19)