Electrostatics - 5
solution: Let q be the charge on inner shell when it is earthed Vinner = 0.
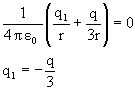
i.e. ![]() charge will flow from inner shell to earth.
charge will flow from inner shell to earth.
Electric dipole: An arrangement of two equal and opposite charges separated by small distance is known as electric dipole.
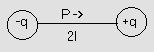
Fig (20)![]()
1) It is a vector quantity.
2) It is directed from –ve charge to +ve charge.
3) The line joining the charges is the axis of dipole.
a) Electric field on the axis (l<<r) = ![]()
Derivation:

Fig (21)
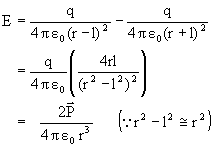
b) On perpendicular bisector = ![]()
Derivation:
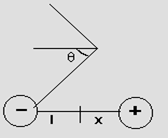
Fig (22)
The component of E cancels out in vertical direction.
Along horizontal.
Enet = E+qCosq + E-qCosq
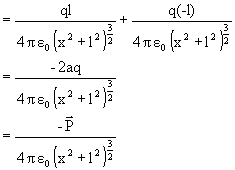
(-ve indicates direction opposite to dipole moment)
If x>> 1
![]()
c) Electric field at any point A(r,0)
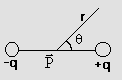
Fig (23)
![]()
Dipole is an external uniform electric field
1) Force on dipole=0.
2) ![]()
![]()
3) Potential energy = -PECos q = -P.E
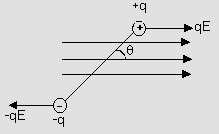
Fig (24)
Q= 0, U will be minimum, stable equilibrium.
Q=1800, U will be maximum, unstable equilibrium.
Illustration:
1) A dipole of dipole moment P lies in uniform electric field with its dipole moment along E. If dipole is rotated through 900, Find work done?
Ui = -P.E = -P.E Cosq = -P.E.
Uf = -PECos900 = 0
Work done = -DU = Ui-Uf =-P.E.
2) A dipole with dipole moment ![]() Cm is aligned at 800 with the direction of a electric field of magnitude 104N/C Calculate magnitude of torque.
Cm is aligned at 800 with the direction of a electric field of magnitude 104N/C Calculate magnitude of torque.
|Z| = PESinq
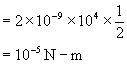
Examples:
1) A charge q = 2´10-6C is placed at (1m, 1m, 1m) and electric field at P (0m,-2m, 1m).
solution:
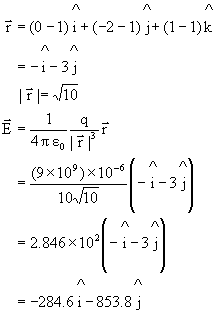
2) Two free particles with charges q and 4q are a distance L apart. A third charge is placed so that system is in equilibrium. Find location, magnitude and size of third charge.
solution: Let new charge be +Q, It will be along the line joining the two charges to balance the forces. Let it be located as shown.
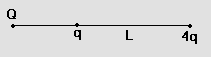 Fig (25)
Fig (25)
Since they are in equilibrium
For q:

For 4q:
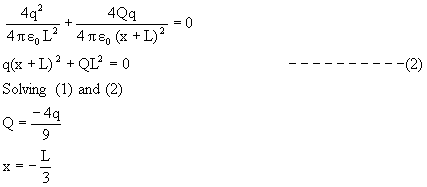
(-ve x means charge will be in middle of the two charges.)
3) A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E then the KE of the particle after time t is.
![]()
solution:
Force = qE
Acceleration = ![]() .
.
![]()
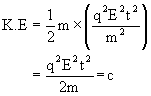
4) P and Q are two concentric metallic spheres. P is positively charged and Q is earthed then
a) Charge density on Q is same as on P.
b) Electric field between P and Q is uniform.
c) Electric potential inside P is zero.
d) Electric field outside Q is zero.
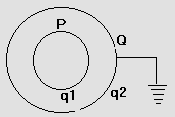
Fig (26)
solution: Let charge on P be q1 and on Q be q2
VQ = 0
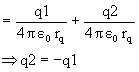
i.e. (a) is false.
(b) Is false as there is potential difference between the two shells and the electric field lines separate outwards.
(c) is false ![]() .
.
(d) is true as q enclosed by Q surface = q2+q1=0.
5) A certain charge Q is divided into two parts q and Q-q. For the maximum Coulomb force between them the ratio (q/Q) is:
1) 1/6, 2) 1/8, 3) 1/4, 4) 1/2
solution:
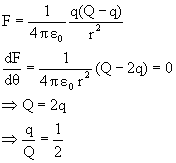
Ans = 4).
6) Three large conducting plate sheets are kept as shown in figure (27). Find electric field a) between (1) and (2), b) between (2) and (3).
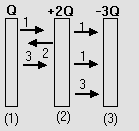
Fig (27)
solution:
a) Between (1) and (2)
Field due to a plate = ![]() .
.
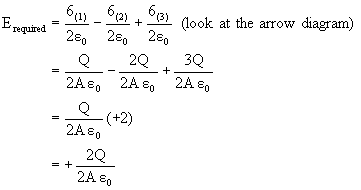
b) Between (2) and (3)
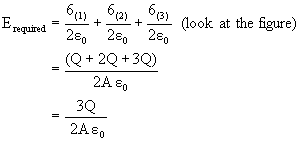
7) A charged particle of mass m=2kg and q=1microcoulomb is thrown from ground at q=300 with speed 30 m/s. There is a horizontal electric field E=107V/m exists. Find the range on horizontal ground of the projectile.
solution:
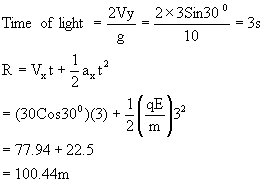
8) A charge q is placed at l/2 distance above a square of length l as shown in figure (28). Find flux through the square.
solution: Consider the charge to be kept in a cube of side l.
Net flux = ![]()
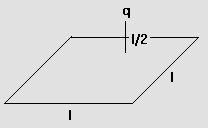
Fig (28)
By symmetry flux through each face = ![]() .
.
9) An alpha particle of KE = 6MeV is heading towards a stationary nucleus of atomic no 30 calculate distance of closet approach.
By conservation of energy:
½ mV2 = Uf-Ui
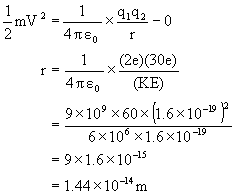
Ans: Since charges are at infinity