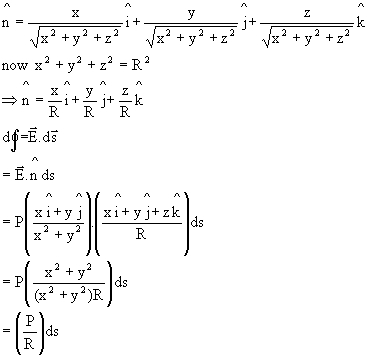Electrostatics - 6

Medium:
Two parallel conducting plates contain charge Q1 and Q2 as shown. Find distribution of charges on four surfaces.

                                                 

                                                               Fig (29)

Consider the Gaussian surface shown.
solution: Two faces lie in the conductor where field is zero, while other two are perpendicular to field direction.
Net charge enclosed = 0
So, the facing inner surface have equal and opposite charges.

                                       

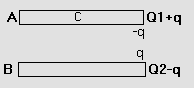
                                                      Fig (30)

Let C be a point in the conductor –

Question:
Why net flux through Gaussian Surface = 0?

                                         

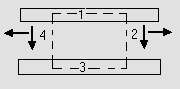
                                                      Fig (31)

There is no field at 1 and 3
Field at 2 and 4 are perpendicular to E.
\E.dA = 0

So, net Flux = 0

Note: Short cut for parallel plates

1)      Charge on facing faces of two plates are equal and opposite

2)      Charge on outermost face = .

Q-2: A curved line charge of density l forming a semi-curve as shown. Find electric field at center.

                                                  

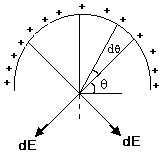
                                                               Fig (32)

Consider the two opposite elements as shown.
The field cancels along x-direction.
Consider an infinitely small element substending angle d

 

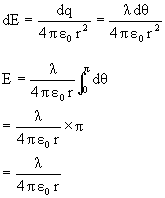
Question:

1)  What would change if the curve were negatively charged?
Ans: The net field will be upwards.

2)  If half of the curve were negatively charged?
Ans: Virtual components cancel while horizontal remains. (Observe yourself)

Q-3: A uniform line charge exist from x =-a to x= a. Find electric field at point P a distance r along the perpendicular bisector.

solution:

                               

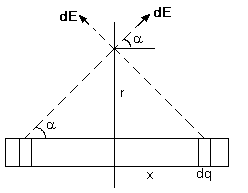
                                                 Fig (33)

Considering the field due to two opposite parts, the field cancels along the horizontal.

Along Vertical:

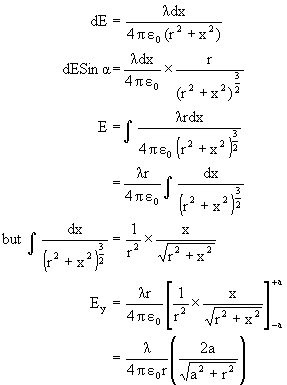
Q-4: A charge Q is uniformly distributed over a spherical volume of radius R. Obtain an expression for the energy of the system.

1)      Inside the sphere(r<R)

     

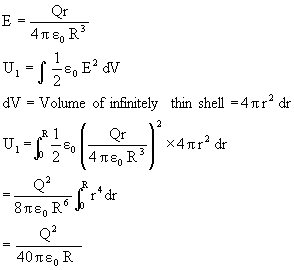
2)      Outside the sphere (r>R)

=

   

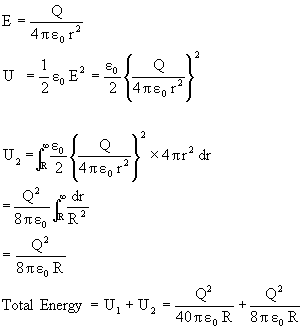
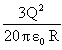
 Question:

solution: Consider a G sphere
            

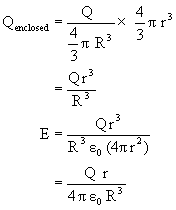
Q-5: Find the potential on the edge of a disc P with surface charge density 6.

Ans:

                                                        

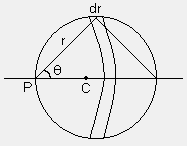
                                                                        Fig (34)           

To calculate the potential at P, the disc is divided as rings with P as center as shown in the figure.
Potential due to element between r and r+dr.

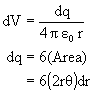
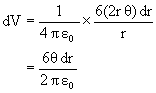
Now r = 2RCosq (as diameter subtends 90⁰ at the edge)
dr = -2RSinqdq.

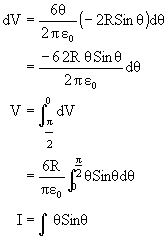
 (Applying Integration by parts)

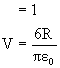
Question:

1) Why were integration limits from p/2 to 0?
Ans: Integration limits were from p/2 to 0 because at p/2, the area around the point would be covered and when angle is zero, the other end of diameter gets covered. Therefore the whole disc is covered.

Q-6: The intensity of an electric field depends on co-ordinates x and y as follows,

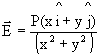
Where P is a constant, find the charge within a sphere of radius R with the center at the origin.

solution: At any point A(x, y, z) on the sphere, a unit vector is perpendicular to the sphere radially outward.

                                   

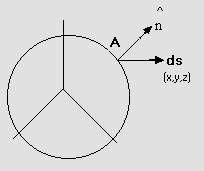
                                              Fig (35)