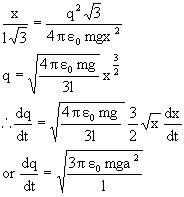Electrostatics - 8

Q-2: Suppose in an insulating medium having dielectric constant K=1, and volume density of positive charge varies with coordinates according to law  . A particle of mass m having positive charge q is placed in the medium at point A (0, y₀) and projected with


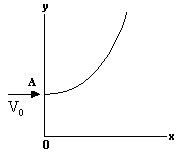
          Fig (38)

Neglecting gravity and frictional resistance of the medium and assuming electric field strength to be zero at y=0, Calculate slope of trajectory of the particle as a function of y.

solution: Since, charge density varies with y coordinates only, therefore in medium an electric field exists which is directed along y axis. To calculate this electric field E(y). Consider a thin layer of medium having thickness dy at a distance y from x-axis as shown in figure.
                                         

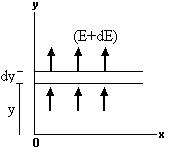
                                                        Fig (39)

Let strength of electric field at positions y and (y+dy) be E and (E+dE) respectively.
Then for area A of the layer,
According to Gauss law


Integrating above equation with limits,
At y=0, E=0 and at y=y, E=E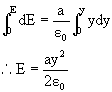

Since frictional resistance of the medium is negligible, therefore there is no force on particle along x-axis or velocity V₀ of particle along x-axis remains constant.
Due to Electric field E, particle accelerates along positive y, this acceleration =

Let y-component of velocity of particle be v

Hence,

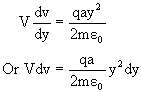
But at point A(y=y₀) y component of velocity is v=0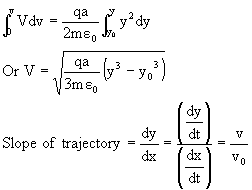

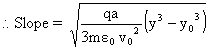
Question:
1) Why there is no force in x-direction?
Ans: The applied electric field is in the y-direction only and it has been mentioned in the question that friction, gravity have to be neglected. Thus there is no force in x-direction.

Q-3: Three identically charged, small sphere each of mass m are suspended from a common point by insulated light strings each of length l the spheres are always on vertices of an equilateral triangle of length of the sides x (<<l). Calculate the rate with which charge on each sphere increases if rate of increase of length of the sides of the equilateral triangle varies as .

solution: Since  is given as  therefore to calculate  first q is to be calculated in terms of x.

Since side of equilateral triangle is x, therefore electrostatic force between two particle is

Positions of particle A, B, C with respect to each other are as shown in figure (40)-A.

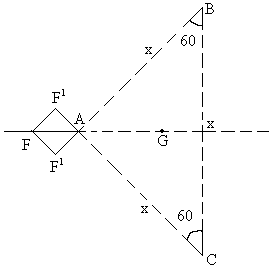
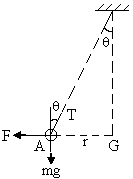
                                Fig (40)-A                                                      Fig (40)-B

Resultant electrostatic force on particle A is

F = 2F¹Cos30⁰ 

In figure (A) G is centroid of triangle.

Distance of centroid G from every particle is

Since G is centroid therefore it always lies vertically below the point of suspension.

Fig (B) shows a vertical plane passing through particle A and centroid G. All of the force acting on particle A is shown in figure (B)

Considering horizontal forces on the particle A,

TSin = F                                                                                      ---------- (1)

For vertical forces TCosq = mg                                                           ---------- (2)

Dividing eq (1) by eq (2)

Since x<<l therefore inclination q of each thread with the vertical is very small.

From equation (3)