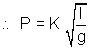Experimental Physics - 2
Derived units:
The units of all other physical quantities which can be obtained from fundamental units are called derived units.
eg: m/s, Kg/m3 etc.
Conversion of units:-
While doing all the calculations in physics, homogenity of units should be Followed. Many times this requires conversion of units. For this we use conversion factor which can be generated as follows:-
Suppose we wish to convert 5 mi/h into m/s
then 1 mile = 1.6 x 103 m
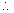factor becomes =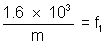 
also ln = 3600 s , factor is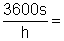
= f2
Complete multiplying factor is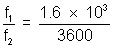
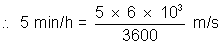
[Remember while finding individual factors, the given unit should be in denominator.]
Multiplication Factor:
To mention Physical Quantities Following standard prefixes for certain power of 10 are used:
Dimensional Analysis:
The dimensions of aphysical quantities are the powers to which the base quantities are raised to represent that quantity "
Dimensions of fundamental Quantities are represented as:
Length [l], mass [M], Time[T], Electric current [A], temperature[K], Luminious intensity[Cd], amount of substance [md]
eg: dimensions of volume = [l]3 0r [m0L3T0] as its unit is m3
force is mass x acceleration units are Kg m/s2 dimension are [MLT-2]
Application of Dimensional Analysis:
(1) In conversion of units from one system to another.
This is based on the fact that product of the numerical value and its corresponding unit is constant.
Numerical value x unit = constant
if unit is changed then numerical value changes
Let dimensions of a quantity be [Ma Lb Tc] and numerical value in first units be n1 [base unit being M1L1T1)
and in seconds unit be n2 [base unit being M2L2T2]
then n1[M1a L1c T12] = n2[M2aL2bT2c
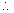n2 = n1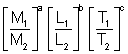
Thus unit conversion can be done.
(ii) Examining dimensional correctness of agiven relation
• For a givenformula to be correct, the dimesion on left hand side and right hand side must be equal.
• Just cdimensional equality doesnot guarentees that formula is correct , but unequal dimensions do state that formula is wrong.
(iii) To establish the relation among various physical quantities
If we know that on what all quantities a particular parameter depends than we can dimensionally work out the correct formula.
• Stokis law has been developed using this principle.
• It is known experimentally that when a ball is in a viscous liquid , then viscous force depends on radius (r) of of the sphere, velocity of the sphere (v) and viscosity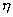
of the liquid
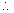F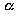 
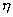(x ry vz)
or F = K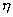x ry vz
examining dimensionally
[MLT-2] = [ML-1T-1]x [L]y[LT-1]2 = [mx L- x + y + z T -x - z]
equating powers we get
x = y = z = 1
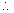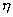F = Krv
K can further be calculated experimentally (K = 6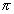
).
In this way, we can easily convert a propwertionality equation in to a formula.
Illustration: The period 'P' of a simple pendlum is the time for one complete swing. How does P depend on the mass m of the bob, the length l of the string and the acceleration due to gravity ?
Solution:- P = Kmx gz ly where k is aconstant
converting the equation into dimensional equation
[T-1] = [M]x [LT-2]2 [L]4
= [mxLZ+yT-2z]
on equating the powers of each dimensions on either side of the equation
Thus z = -1/2, y = 1/2, x = 0
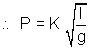
The units of all other physical quantities which can be obtained from fundamental units are called derived units.
eg: m/s, Kg/m3 etc.
Conversion of units:-
While doing all the calculations in physics, homogenity of units should be Followed. Many times this requires conversion of units. For this we use conversion factor which can be generated as follows:-
Suppose we wish to convert 5 mi/h into m/s
then 1 mile = 1.6 x 103 m
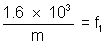
factor becomes = also ln = 3600 s , factor is
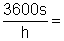= f2Complete multiplying factor is
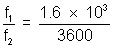
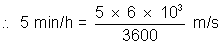
[Remember while finding individual factors, the given unit should be in denominator.]
Multiplication Factor:
To mention Physical Quantities Following standard prefixes for certain power of 10 are used:
| Power of 10 | Prefix | Symbol |
| + 12 + 9 + 6 + 3 - 2 - 3 - 6 - 9 - 12 |
Tera Giga Mega Kilo Centi milli micro nano pico |
T G M K C m 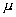 n P |
Dimensional Analysis:
The dimensions of aphysical quantities are the powers to which the base quantities are raised to represent that quantity "
Dimensions of fundamental Quantities are represented as:
Length [l], mass [M], Time[T], Electric current [A], temperature[K], Luminious intensity[Cd], amount of substance [md]
eg: dimensions of volume = [l]3 0r [m0L3T0] as its unit is m3
force is mass x acceleration units are Kg m/s2
dimension are [MLT-2]Application of Dimensional Analysis:
(1) In conversion of units from one system to another.
This is based on the fact that product of the numerical value and its corresponding unit is constant.
Numerical value x unit = constant
if unit is changed then numerical value changesLet dimensions of a quantity be [Ma Lb Tc] and numerical value in first units be n1 [base unit being M1L1T1)
and in seconds unit be n2 [base unit being M2L2T2]
then n1[M1a L1c T12] = n2[M2aL2bT2c
n2 = n1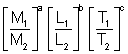Thus unit conversion can be done.
(ii) Examining dimensional correctness of agiven relation
• For a givenformula to be correct, the dimesion on left hand side and right hand side must be equal.
• Just cdimensional equality doesnot guarentees that formula is correct , but unequal dimensions do state that formula is wrong.
(iii) To establish the relation among various physical quantities
If we know that on what all quantities a particular parameter depends than we can dimensionally work out the correct formula.
• Stokis law has been developed using this principle.
• It is known experimentally that when a ball is in a viscous liquid , then viscous force depends on radius (r) of of the sphere, velocity of the sphere (v) and viscosity
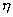of the liquid F 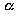(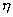x ry vz)or F = K
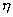x ry vz examining dimensionally
[MLT-2] = [ML-1T-1]x [L]y[LT-1]2 = [mx L- x + y + z T -x - z]
equating powers we get
x = y = z = 1
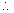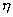F = KrvK can further be calculated experimentally (K = 6
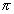).In this way, we can easily convert a propwertionality equation in to a formula.
Illustration: The period 'P' of a simple pendlum is the time for one complete swing. How does P depend on the mass m of the bob, the length l of the string and the acceleration due to gravity ?
Solution:- P = Kmx gz ly where k is aconstant
converting the equation into dimensional equation
[T-1] = [M]x [LT-2]2 [L]4
= [mxLZ+yT-2z]
on equating the powers of each dimensions on either side of the equation
Thus z = -1/2, y = 1/2, x = 0