Experimental Physics - 3

Significant Figures:-
In all types of measurement the reported measurement consists of Numbers. The digits that we report consists of certain digits (which are measurable by an instrument) and doubtful digits (which are lesser than the least value an instrument an measure). All these digits including the doubtful digit are called signifiant digits.

Dumb Question:- What excately are doubtful digits ?
Ans:- Doubtfull digits are the uncertain digit. For a simple scale, the smallest division is of 1mm. While measuring a length of line if one end of line is at 0 and other end is slightly above 8mm mark, then we report answer is 0.8cm here 8 is uncertain. In all instrument the smallest value which it can measure is the uncertain place and this smallest value is called LEAST COUNT OF INSTRUMENT.
s
Rules for Significantnt figures:-
• All the non - zero digits are significant.

• All the zeros between two non - zero digits are significan, iorrespective of the position of decimal point. eg. 706.06 has 5 significant figures.

• If the number is less than 1, the zeros on the right of decimal point but to the left of first non - zero digit are not significant.
eg: 0.002705 underlined zeros are insignificant.

• All the zeros to the right of the last non - zero digit (terminal trailing zeros) in a number without a decimal point are not significant.
20m, 2000cm, 2000mm all have just 1 significant figure.
*Note:- But if there are values as measured by same instrument then they become significant.

• The trailing zeros in a number with a decimal point are significant.
eg: 3.700 or 0.004700 have 4 significant figures.

Dumb Question:- Does the choice of units change the number of significant figures ?
Ans:- No changing units doesn’t change the number of significant figures. eg: the length 4.705 cm has 4 significant figures, same value can be written as 0.04705m, unit has changed but number of significant figure have remained same.
If however the values given one as per the measurement of an instrument than this rule is not applicable and in that case the rule holds if even after changing the units we mention the result upto the least count of instrument.

Significant digits in algebraic operations:-
• Following rule are used to determining the number of significant digits, when an algewbraic operatins is performed:-

• In addition or substraction, the final result should retain as many decimal places as are there in the number with the least decimal place.
for eg: 514.72 + 213.1 = 727.82
but the answer to be reported is 727.8
[for getting the correct last position, necessary rounding off must be done.]

• In multiplication or division, the number of significant digits in the final result should be equal to the number of significant digits in the quantity, which has the minimum number of significant digits.
eg: An object has mass 4.237g and volume 2.51 cm3, than its density is 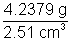= 1.6486 g/cm³
but the answer to be reported is 1.65 g/cm³ [3 significant igures]

Rules for Rounding off:-
(i) If the digits next to the last significant (uncertain) digits is more than 5, the digit to be rounded is increased by 1.

(ii) If the digits next to be rounded is less than 5, the digit to be rounded is left unchanged.

(iii) If the digit next to the one rounded is 5, then the digit to be rounded is increased by 1 if it is odd and left unchanged if it is even.

Illustration:-
A reactangular plate has a length of (21.3 ± 0.2)cm and a width of (9.80 ± 0.10)cm. Find the area of the plate and the uncertaininty in the calculated area.
Solution:- Area = lb = (21.3 ± 0.2) x (9.80 ± 0.10) cm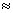
(21.3 x 9.80 ± 21.3 x 0.10 ± 0.2 x 9.80) cm²
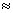(209 ± 4) cm²

Dumb Question:- Why was the product 0.2 x 0.10 left in the above computation ?
Ans:- Let numbers be A = a + a and B = b + b
then A x B = (A + a) x (b + b) = ab + a x b + b x a + a x b
the product a x b is too small and has high degree of uncertainity, as it involves product of two uncertain quantities, hence it is always dropped.

Error analysis:
• Least count:- The least value of a quantity, which the instrument can measure accurately, is called the least count of the instrument.

• Error:- The measured value is always different from true value. The uncertaininity involved in the measurement has certain value which is called error.

• Accuracy and Precision:- The accuracy of a measurement is a measure of how close the measured value is to the true value of the quantity. Precission tells us to what resolution or limit the quantity is measured.

• Absolute Error:- The magnitude of the difference between the true value of the quantity and the individual measurement value is called the absolute error of the measurement.
s [True value is taken to be arithematic mean of all the observation i.e. x means when x_mean = ]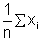
absolute errors x₁ = x_mean - x₁ = x₂ = x_mean - x₂ and so on.
Absolute error can be +ve as well as -ve.

• Absolute Mean Error:- The Average of the mod of errors is called the average/mean error
x_mean = (|x₁| + |x₂| + |x₃| + ……………. + |x_n|)/n

• Relative Error:- The relativr error is the ratio of the mean Absolute error x_mean to he mean value x_meanof the quantity measured.
Realtive error = x_mean/x_mean

• Percentage Error:- When the relative error is expressed in percent, it is called percentage error.
Thus perentage error = (x_mean/x_mean) x 100%