Fluids that include liquids and gases play a vital role in our daily lives as we breathe and drink them. Cars run on fluid (Petrol, diesel), Oceans and rivers are full of fluid (water), battery, AC’s, refrigerators too contain fluids (CFC’s etc)
DEFINITION
A fluid is a substance that can flow and conform to the boundaries of any container containing it. This is because fluid can not sustain a force that is tangential to its surface. More over fluid flows because it can not with stand a shearing stress.
DENSITY
To find the density r of a fluid at any point, we isolate a small volume element DV around that point and measure the mass Dm of the fluid contained within that element.
The density is then
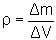
For uniform density we may write as
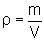(Uniform density)
Where m and V are the mass and Volume of the sample
S.I unit of density is Kgcm-3
Density is a Scalar quantity.
PRESSURE IN A FLUID
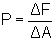Or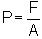 
(pressure of uniform force on flat area).
S.I unit of pressure is N/m2 called Pascal (Pa).
Pressure is a scalar quantity.
The atmosphere (atm) exerts certain pressure at a point depending on the column or height of atmosphere lying above that point.
The average pressure of the atmosphere at sea level is known as atmospheric pressure (atm) and
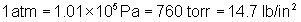
Now onwards we shall assume that the liquids we deal with are incompressible and non viscous (though they are not strictly).
VARIATION OF PRESSURE WITH HEIGHT (DEPTH):
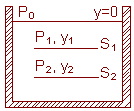
Fig (1)
Let us consider a cylinder filled with water. Consider surfaces S1 and S2 on which pressure due to water is P1 and P2 respectively at heights y1 and y2 respectively from the top of surface i.e. y=0 then P1 and P2 can be related as
P2 = P1+rg (y1-y2) --------------------- (1)
Where r = Density of water (or other liquid).
g = Acceleration due to gravity (9.8 m/sec2).
The equation can be used to find pressure both in a liquid (as a function of depth) and in the atmosphere (as a function of altitude or height).
Thus, pressure at depth h can be taken as P where
P = P0 + rgh ------------------------ (2)
Where P0 = Pressure on the surface where h = 0.
Note: The pressure at any point in a fluid in static equilibrium depends on the depth of that point but not on any horizontal dimension of the fluid or its container.
Thus equation (2) holds no matter what the shape of the container.