FLOATING:
When a body floats in a fluid, the magnitude Fb of the buoyant force on the body is equal to the magnitude Fg of the gravitational force on the body.
Thus, Fb = Fg (floating).
Also, Fb = mfg = Fg.
Where, mf = mass of the fluid that is displaced by the body.
APPERENT WEIGHT IN A FLUID:
If an object is placed inside a fluid then,
(Apparent weight) = (Actual weight) – (Buoyant force).
FLOW OF IDEAL FLUIDS:
An ideal fluid is incompressible and lacks viscosity, and its flow is steady and irrotational. A stream line is the path followed by an individual fluid particle.
EQUATION OF CONTINUITY:
It means that total mass of fluids going into the tube through any cross-section should be equal to the total mass coming out of the same tube from any other cross section in the same time.
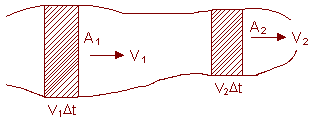
Fig (6)
Thus A1V1Dt = A2V2Dt (as shown in figure (6))
Or A1V1 = A2V2.
The product of the area of cross section and the speed remains the same at all points of a tube of flow. This is called the “equation of continuity” and expresses the law of conservation of mass in fluid dynamics.
BERNOULLI’S EQUATION:
Bernoulli’s equation relates the speed of a fluid at a point the pressure at that point and the height of that point above a reference level. It is just the application of work-energy theorem in the case of fluid flow.
We here consider the case of irrotational and steady flow of an incompressible and non viscous liquid.
According to Bernoulli’s Equation,
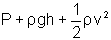= Constant.
Application of Bernoulli’s Equation:
a) Hydrostatics:
If the speed of the fluid is zero every where, we get the situation of hydrostatics. Putting V1 = V2 = 0 in the Bernoulli’s equation
P1+rgh1 = P2+rgh2.
P1 - P2 = rg (h1-h2). As expected from hydrostatics.