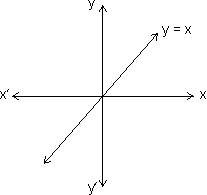functions-and-graphs-1
Functions:
Let A B be two non empty sets & F is a relation which associates each elemenet of set A with unique element of set B, then F is c/d a function from A to B.
B be two non empty sets & F is a relation which associates each elemenet of set A with unique element of set B, then F is c/d a function from A to B.
Set A is called domain of F & B be the co domain of F.
Set of elements of B, which are images of elements of set A is c/d range of F.
F : A B ("F is function of A into B")
B ("F is function of A into B")
If a A then element in B which is assigned to 'a' is called image of 'a' & denoted by F(a).
A then element in B which is assigned to 'a' is called image of 'a' & denoted by F(a).
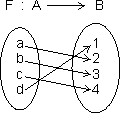
let A = {a, b, c, d}, B = {1, 2, 3, 4, 5}
So, F(a) = 2, F(b) = 3, F(c) = 5, F(d) = 1
Dumb Question: What is non empty set ?
Ans: A set which contain at least one element
eg. A = {1, 2} is non empty set but B = { } is empty set.
No. of Function (or Mapping) From A to B:
Let A = {x1, x2, x3, .......... , xm} F : A B
B
& B ={y1, y2, y3, .......... , yn}
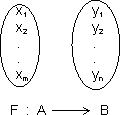
Then if each elemenet in set A has n images in set B.
Thus, total no. of functions from A to B = nm
Dumb Question: How total no. of function from A to B = nm ?
Ans: x1, element in set A take n images
x2 element in set A take n images
.............................................
.............................................
xm can take n images.
 Total no. of function from A to B
Total no. of function from A to B
 n x n x ............... m times = nm
n x n x ............... m times = nm
Domain: Domain of y = f(x) is set all real x for which f(x) is defined (real).
How to find Domain:
(i) Expression under even root (i.e. square root, 4th root) 0
0
(ii) Denominator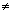 0
0
(iii) If domain of y = (x) & y = y(x) are D1 & D2 respectivly then domain of f(x) ± y(x) of f(x).g(x) is D1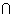 D2.
D2.
(iv) Domain of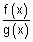 is D1
is D1 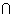 D2 - {g(x) = 0}.
D2 - {g(x) = 0}.
Illustration: Find domain of single valued function y = f(x) given by eq. 10x + 10y = 10.
Ans: 10x + 10y = 10 10y = 10 - 10x
10y = 10 - 10x
 y = log10(10 - 10x) {am = b
y = log10(10 - 10x) {am = b  m = logab}
m = logab}
Now, 10 - 10n > 0
 101 > 10x
101 > 10x  1 > x
1 > x
domain x (-
(-  , 1)
, 1)
Dumb Question: What is single value Function ?
Ans. For every point of domains, these is unique image only.
Range: Range of y = f(x) is collection of all output & {F(x)} corresponding to each real no. is domain.
How to find range:
First of all final domain of y = f(x)
(i) If domain Finite no. of points
Finite no. of points  range
range  set of corresponding f(x)values.
set of corresponding f(x)values.
(ii) If domain R or R - {some finite points}
R or R - {some finite points}
Then express x in terms of y. From this find y for x to be defined. (i.e. find values of y for which x exists)
(iii) If domain a finite interval, find least and greatest value for range using mono tonicity.
a finite interval, find least and greatest value for range using mono tonicity.
Illustration: Find range of function y = loge(3x2 - 4x + 5).
Ans: y is difind if 3x2 - 4x + 5 > 0
[Dumb Question: Why 3x2 - 4x + 5 > 0 ?
Ans: ln x is defind only if x > 0]
if x is 0 ln x = - & for - ve x
& for - ve x
ln is not defind,
D = 16 - 4 x 3 x 5 = - 44 < 0
& coeff. of x2 = 3 > 0
 3x2 - 4x + 5 > 0
3x2 - 4x + 5 > 0 v x  R
R
 domain
domain  R
R
y = loge(3x2 - 4x + 5) 3x2 - 4x + 5 = ey
3x2 - 4x + 5 = ey
 3x2 - 4x + (5 - ey) = 0
3x2 - 4x + (5 - ey) = 0
Since x is real, So, D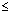 0
0
(- 4)2 - 4(3)(5 - ey) > 0 ey >
ey > 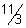
 y
y 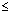 log
log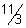
 range
range  [log
[log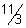 ,
,  )
)
1. Constant Function: If range of function f consists of only one no. then f is c/d constant function.
Range = { a }
domain x R
R
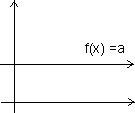
2. Polynomial function: A function y = f(x) = a0xn + a1xn- + ...... + an where a0, a1, ....... an are real constants & n is non -ve integer, then f(x) is c/d polynomial function. If a0 = 0, then n is degree of polynomial function.
Graph of f(x) = x2
f(x) = x2 is called square function. Domain R
R
Range R+
R+ 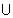 {0} or [0,
{0} or [0,  ]
]

Graph of f(x) = x3:
f(x) = x2 is cube function
domain R
R
Range R
R
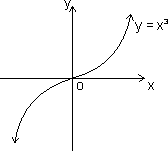
(3) Rational Function: It is ratio of two polynomials
Let P(x) = a0xn + a1xn - 1 + .......... + an
Q(x) = b0xm + b1xm - 1 + .......... + bm
Then f(x) =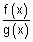 is a rational function if Q(x)
is a rational function if Q(x) 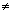 0
0
Domain R
R  {x | Q(x) = 0}
{x | Q(x) = 0}
i.e. Domain R except those points for which denomiator = 0
R except those points for which denomiator = 0
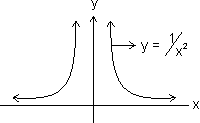
Graph of f(x) =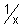
f(x) =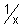 is called reciprocal function with coordinate axis as asymptotes.
is called reciprocal function with coordinate axis as asymptotes.
Domain R - {0}
R - {0}
Range R - {0}
R - {0}
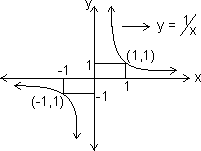
Graph of f(x) =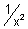
f(x) =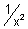
Domain R - {0}
R - {0}
Range (0,
(0,  )
)
Dumb Question: For y =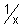 , how domain & range is R - {0} ?
, how domain & range is R - {0} ?
Ans: For domains
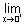 f(x) = +
f(x) = +  &
& 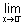 f(x) = -
f(x) = - 
So, f(x) is not defined at x = 0
Similarly for Range
as x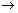 ±
± 
 f(x)
f(x) 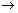 0
0
But we exclude ±
So, Range R - {0}
R - {0}
(4) Irrational Function: Algebraic function containing trems having non-integral rational powers of x are c/d irrational functions.
Graph of f(x) =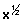
f(x) =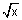 Domain
Domain  R+
R+  {0} or {0,
{0} or {0,  )
)
Range R+
R+  {0} of [0,
{0} of [0,  )
)
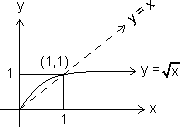
Grafh of f(x) =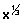
f(x) =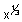
domains R
R
Range R
R
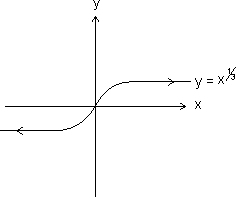
(5) Identity Function: The function y = f(x) = x for all x R c/d identity function on R
R c/d identity function on R
Domain R
R
Range R
R
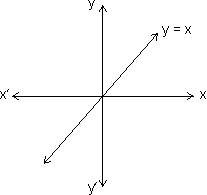
Let A
 B be two non empty sets & F is a relation which associates each elemenet of set A with unique element of set B, then F is c/d a function from A to B.
B be two non empty sets & F is a relation which associates each elemenet of set A with unique element of set B, then F is c/d a function from A to B.Set A is called domain of F & B be the co domain of F.
Set of elements of B, which are images of elements of set A is c/d range of F.
F : A
 B ("F is function of A into B")
B ("F is function of A into B")If a
 A then element in B which is assigned to 'a' is called image of 'a' & denoted by F(a).
A then element in B which is assigned to 'a' is called image of 'a' & denoted by F(a).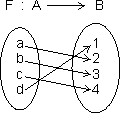
let A = {a, b, c, d}, B = {1, 2, 3, 4, 5}
So, F(a) = 2, F(b) = 3, F(c) = 5, F(d) = 1
Dumb Question: What is non empty set ?
Ans: A set which contain at least one element
eg. A = {1, 2} is non empty set but B = { } is empty set.
No. of Function (or Mapping) From A to B:
Let A = {x1, x2, x3, .......... , xm} F : A
 B
B& B ={y1, y2, y3, .......... , yn}
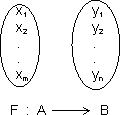
Then if each elemenet in set A has n images in set B.
Thus, total no. of functions from A to B = nm
Dumb Question: How total no. of function from A to B = nm ?
Ans: x1, element in set A take n images
x2 element in set A take n images
.............................................
.............................................
xm can take n images.
 Total no. of function from A to B
Total no. of function from A to B n x n x ............... m times = nm
n x n x ............... m times = nmDomain: Domain of y = f(x) is set all real x for which f(x) is defined (real).
How to find Domain:
(i) Expression under even root (i.e. square root, 4th root)
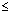 0
0(ii) Denominator
 0
0(iii) If domain of y = (x) & y = y(x) are D1 & D2 respectivly then domain of f(x) ± y(x) of f(x).g(x) is D1
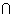 D2.
D2.(iv) Domain of
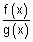 is D1
is D1 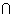 D2 - {g(x) = 0}.
D2 - {g(x) = 0}.Illustration: Find domain of single valued function y = f(x) given by eq. 10x + 10y = 10.
Ans: 10x + 10y = 10
 10y = 10 - 10x
10y = 10 - 10x y = log10(10 - 10x) {am = b
y = log10(10 - 10x) {am = b  m = logab}
m = logab}Now, 10 - 10n > 0
 101 > 10x
101 > 10x  1 > x
1 > xdomain x
 (-
(-  , 1)
, 1)Dumb Question: What is single value Function ?
Ans. For every point of domains, these is unique image only.
Range: Range of y = f(x) is collection of all output & {F(x)} corresponding to each real no. is domain.
How to find range:
First of all final domain of y = f(x)
(i) If domain
 Finite no. of points
Finite no. of points  range
range  set of corresponding f(x)values.
set of corresponding f(x)values.(ii) If domain
 R or R - {some finite points}
R or R - {some finite points}Then express x in terms of y. From this find y for x to be defined. (i.e. find values of y for which x exists)
(iii) If domain
 a finite interval, find least and greatest value for range using mono tonicity.
a finite interval, find least and greatest value for range using mono tonicity.Illustration: Find range of function y = loge(3x2 - 4x + 5).
Ans: y is difind if 3x2 - 4x + 5 > 0
[Dumb Question: Why 3x2 - 4x + 5 > 0 ?
Ans: ln x is defind only if x > 0]
if x is 0 ln x = -
 & for - ve x
& for - ve xln is not defind,
D = 16 - 4 x 3 x 5 = - 44 < 0
& coeff. of x2 = 3 > 0
 3x2 - 4x + 5 > 0
3x2 - 4x + 5 > 0  R
R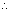 domain
domain  R
Ry = loge(3x2 - 4x + 5)
 3x2 - 4x + 5 = ey
3x2 - 4x + 5 = ey 3x2 - 4x + (5 - ey) = 0
3x2 - 4x + (5 - ey) = 0Since x is real, So, D
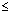 0
0(- 4)2 - 4(3)(5 - ey) > 0
 ey >
ey > 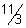
 y
y 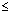 log
log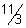
 range
range  [log
[log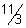 ,
,  )
)CLASSIFICATION OF FUNCTIONS
1. Constant Function: If range of function f consists of only one no. then f is c/d constant function.
Range = { a }
domain x
 R
R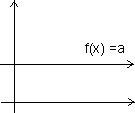
2. Polynomial function: A function y = f(x) = a0xn + a1xn- + ...... + an where a0, a1, ....... an are real constants & n is non -ve integer, then f(x) is c/d polynomial function. If a0 = 0, then n is degree of polynomial function.
Graph of f(x) = x2
f(x) = x2 is called square function. Domain
 R
RRange
 R+
R+  {0} or [0,
{0} or [0,  ]
]
Graph of f(x) = x3:
f(x) = x2 is cube function
domain
 R
RRange
 R
R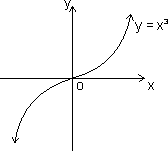
(3) Rational Function: It is ratio of two polynomials
Let P(x) = a0xn + a1xn - 1 + .......... + an
Q(x) = b0xm + b1xm - 1 + .......... + bm
Then f(x) =
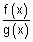 is a rational function if Q(x)
is a rational function if Q(x) 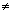 0
0Domain
 R
R  {x | Q(x) = 0}
{x | Q(x) = 0}i.e. Domain
 R except those points for which denomiator = 0
R except those points for which denomiator = 0Graph of f(x) =
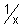
f(x) =
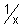 is called reciprocal function with coordinate axis as asymptotes.
is called reciprocal function with coordinate axis as asymptotes.Domain
 R - {0}
R - {0}Range
 R - {0}
R - {0}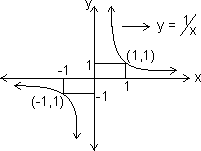
Graph of f(x) =
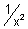
f(x) =
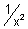
Domain
 R - {0}
R - {0}Range
 (0,
(0,  )
)
Dumb Question: For y =
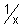 , how domain & range is R - {0} ?
, how domain & range is R - {0} ?Ans: For domains
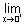 f(x) = +
f(x) = +  &
& 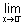 f(x) = -
f(x) = - 
So, f(x) is not defined at x = 0
Similarly for Range
as x
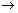 ±
± 
 f(x)
f(x) 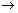 0
0But we exclude ±

So, Range
 R - {0}
R - {0}(4) Irrational Function: Algebraic function containing trems having non-integral rational powers of x are c/d irrational functions.
Graph of f(x) =
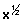
f(x) =
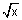 Domain
Domain  R+
R+ 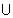 {0} or {0,
{0} or {0,  )
)Range
 R+
R+ 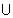 {0} of [0,
{0} of [0,  )
)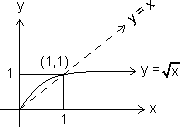
Grafh of f(x) =
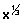
f(x) =
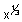
domains
 R
RRange
 R
R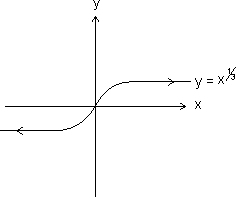
(5) Identity Function: The function y = f(x) = x for all x
 R c/d identity function on R
R c/d identity function on RDomain
 R
RRange
 R
R