Sketch of curve y = cos-1(4x3 - 3x)
Domain 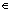 [-1, 1] range [-1, 1] range 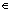 [0, [0, 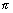 ] ]
Let x = cos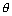
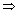 y = cos-1(cos3 y = cos-1(cos3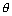 ) = ) = 
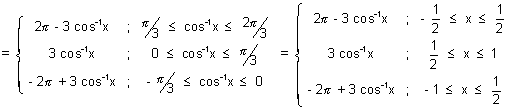
This curve has sharp edge at x = ± 1/2. So, not differentiable at x = ± 1/2.
Dumb Question: Why y = cos-1(cos3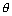 ) = 2 ) = 2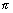 - 3 - 3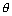 if if 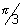 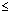 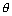 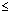 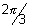 . .
Ans: Range of y 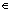 [0, [0, 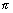 ) if ) if 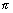  3 3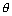 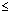 2 2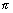 . So, it s out of range so, it make it within range, we substract it from 2 . So, it s out of range so, it make it within range, we substract it from 2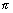
and cos(2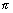 - 3 - 3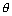 ) = cos3 ) = cos3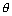
Odd and Even functions: A function is said to be an odd function if, f(-x) = - f(x) for all x.
Graph of odd function is symetrical in opposite quadrants. eg.
Even function: A function f(x) is said to be an even of f(-x) = f(x) for all x.
Graph is symmetrical about y-axis.
Properties:
(i) Product of two odd functions or two even functions is an even function.
(ii) Product of odd and even function is an odd function.
(iii) Every function y = f(x) can be expressed as sum of an even and odd function.
Illustration: IF f is an even function, find real values of x satisfying eq. f(x) = f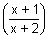
Ans: Since f(x) is even function
 f(x) = f(-x) f(x) = f(-x)
Thus, x = 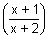 or - x = or - x = 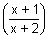
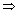 x2 + x - 1 = 0 or - x2 - 3x - 1 = 0 x2 + x - 1 = 0 or - x2 - 3x - 1 = 0
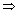 x = x = 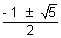 or x = or x = 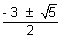
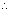 x = x = 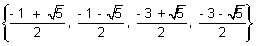
Periodic Function: A function f(x) is said to be periodic function if, there exists a +ve real no. such that,
f(x + T) = f(x), v x 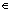 R R
Then, f(x) is periodic with period T, where T is least +ve value.
eg. sin x is priodic with period 2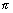 . .
Illustration: Prove that f(x) = x - [x] is periodic function. Also find its period.
Ans: Let T > 0,
Then, f(x + T) = f(x), v x 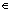 R R
 (x + T) - [x + T] = x - [x] (x + T) - [x + T] = x - [x] v x 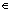 R R
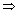 [x + T] - [x] = T v x [x + T] - [x] = T v x 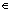 R R
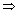 T = 1, 2, 3, 4, .............. {Since substruction of two integer} T = 1, 2, 3, 4, .............. {Since substruction of two integer}
Smallest value of T satisfying
f(x + T) = f(x) is 1
So, period with period 1.
Properties of periodic function:
(i) If f(x) is periodic with period T, then,
c.f(x), f(x + c) & f(x) ± c is periodic with period T.
eg. if sin x has period 2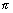 . Then f(x) = 5 sinx + 4 is also periodic with period 2 . Then f(x) = 5 sinx + 4 is also periodic with period 2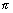 . .
(ii) If f(x) is periodic with period T, then, kf(cx + d) has period 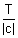
f(x) = 7 sin2x - 12 has period 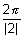 = = 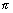 as sinx is periodic with period 2 as sinx is periodic with period 2 . .
(iii) If f1(x), f2(x) are periodic functions with periods T1, T2 respectively then; h(x) = af1(x) ± bf2(x) has period as

LCM of 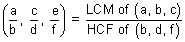
Note: LCM of rational and irrational is not possible. eg. 2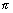 is irrational & 1 is rational. is irrational & 1 is rational.
Composite Function:
LEt two function,
f : x 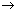 Y1 and g : Y1 Y1 and g : Y1 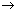 Y Y
Let another function h : X 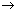 Y Y
Such that
h(x) = g(f(x)) = (gof)(x)
domain (gof) = {x : x 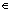 domain (f), f(x) domain (f), f(x) 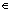 domain (a)} domain (a)}
domain fog(x) = {x : x 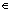 domain (g), g(x) domain (g), g(x) 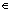 domain f} domain f}
gof exist iff range of f 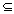 domain of g domain of g
fog exist iff range of g 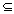 domain of f. domain of f.
Properties of composite function:
(i) f is even, g is even 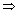 fog is even function. fog is even function.
(ii) f is odd, g is odd 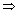 fog is odd function. fog is odd function.
(iii) f is even, g is odd 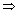 fog is even function. fog is even function.
(iv) f is odd, g is even 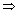 fog is even function. fog is even function.
Illustration: Let g(x) = 1 + x - [x] & f(x) = 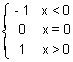 . Find fog(x). . Find fog(x).
Ans: g(x) = 1 + x - [x] = 1 {x}
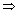 g(x) is greater than J. g(x) is greater than J.
So, f(g(x)) = 1. since f(x) = 1 for all x > 0
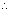 f(g(x)) = 1 for all x f(g(x)) = 1 for all x  R. R.
Mapping of function: A function exists only if,"to every element in domain there exists unique image in codomain.
f : A 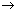 B B
One - One Mapping (Injective): A function f: A  B is said to bwe one-one mapping if different elements of A have different images in B. B is said to bwe one-one mapping if different elements of A have different images in B.  no two elements of set A can have same 'f' image no two elements of set A can have same 'f' image
eg.
f(x) is one-one
Methods to find one-one mapping:
(1) Graphically: A fun. is one-one if no line 11 to x-axis meets graph of function at more than one point.
By Calculus: If f(x) is function and if f'(x) 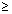 0 0 v x 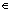 domain i.e. increasing or f'(x) domain i.e. increasing or f'(x) 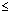 0 0 v x 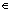 domain i.e. decreasing, then one-one. domain i.e. decreasing, then one-one.
No. of one-one Mapping: If A & B are finite sets having m & h elements, then, no. of one-one function from A to B
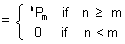
Dumb Question: How No. of one-one mapping is nPm if n 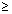 m. m.
Ans: x1 can take n images
x2 can take (n - 1) images
.....................................
.....................................
.....................................
.....................................
xm can take (n - m + 1) images
 No. of mapping = n(n - 1)(n - 2) ............... (n - m + 1) = nPm No. of mapping = n(n - 1)(n - 2) ............... (n - m + 1) = nPm
Many one Mapping: A mapping f : A  B is many one if two or more elements of set A have the same image in B. B is many one if two or more elements of set A have the same image in B.
i.e. f(x3) = f(x4) = y3
Onto Function (Surjective): If function f : A 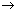 B is such that each element of B is the 'f' image of at least one element in A. B is such that each element of B is the 'f' image of at least one element in A.
i.e. range of f = codomain 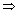 f(A) = B f(A) = B
Into Function: A function of f : A 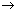 B is into if there exists an element in B having no preimage in A. B is into if there exists an element in B having no preimage in A.
No. of one-one onto mapping (bijection): If A & B are finite sets & f : A 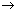 B is a bijection. B is a bijection.
Then A & B have same no. of elements.
Total no. of bijection A  B = n ! B = n !
Dumb Question: How total no. of bijection A  B = n ! ? B = n ! ?
Ans: x1 can take n images
x2 can take (n - 1) images
x3 can take (n - 2) images
.....................................
.....................................
.....................................
xm can take 1 images
 No. of mapping = n(n - 1)(n - 2) ............... 1 = n ! No. of mapping = n(n - 1)(n - 2) ............... 1 = n !
|
|
| |
|
|