functions-and-graphs-6

Functions:

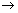
Illustration: Find no. of surjection from A B
A = {1, 2, 3, 4} & B = {a, b}

Ans:

   1 2 images
   2 2 images
   3 2 images
   4 2 images
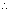
Total no. of function = 2 x 2 x 2 x 2 = 2⁴
But there are two function f(x) = a for all x A & g(x) = b for all x A are not surjective.
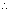
Total no. of surjection from A to B = 2⁴ - 2 = 14


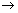
Inverse function: Let f : A B be one-one & onto function then there exists a unique function.


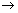
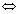
g : B A such that f(x) = y   g(y) = x, v x A & y B
Then g is c/d inverse of F.
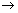
So, g = f^-1 : B A = {(f(x), x) | (x, f(x) f}
Domain of f = {1, 2, 3, 4} = range of f^-1
Range of f = {2, 4, 6, 8} = domain of f^-1.


Illustration: If f(x) = 3x - 5, then find f^-1(x).

Ans: f(x) = 3x - 5 which linear function so bijective.
Let f(x) = y   Y = 3x - 5
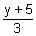
x =   f^-1(y) =
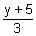
f^-1(x) =

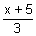Note: (1) Graph of y = f(x) and y = f^-1(x) are mirror images to each other.

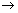
(2) If f : A B & g : B C are two bijections, then gof : A C is bijection & (gof)^-1 = (f^-1og^-1).

(3) If fog = gof then either f^-1 = g or g^-1 = f and (fog)(x) = (gof)(x) = (x)




Q.1. Find domain of f(x) = log₁₀log₁₀(1 + x³)

Ans: Let   log₁₀(1 + x³) = y
f(x) = log₁₀y   y > 0
log₁₀(1 + x³) > 0   (1 + x³) > 10⁰
x³ > 0   x (0, )


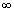
Q.2. Find domain of y =

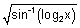
Ans: Let log₂x = z
z is defined if x > 0 .......................................... (i)
and - 1 z 1   or   - 1 log₂x 1
1/2 x 2 ................................................. (ii)
But y is defined if
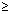
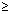
    sin^-1z 0   or   sin^-1log₂(x) 0 ..................... (iii)
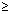
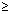
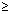
log₂x 0   x 2⁰   x 1 .................. (iv)
From (i), (ii) & (iv)
    1 x 2
domain x [1, 2]


Q.3. Find values of 'a' for which f(x) = tan^-1(x² - 18x + 9) > 0 for x R.

Ans: f(x) > 0 v x R
x² - 18x + a > 0 v x R
    ax² + bx + c > 0   if   D < 0   &   a > 0
    D = (18)² - 49 < 0   a > 81
a (81, )


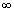
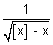
Q.4. f(x) =   find domain of f9x).

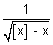
Ans: f(x) =   exists if
[x] - x > 0   [x] > x
But by definition of greatest integer function
[x] x   as   x = [x] + {x}
So, it is not possible that [x] > x
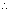
domain f(x) =


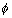
Q.5. Solve   4{x} = x + [x]

Ans: x = [x] + {x}
       4{x} = [x] + {x} + [x]   {x} =
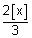
But   0 {x} < 1
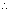
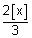
0 < 1   0 [x] < 3/2
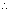
[x] = 0 or 1
If [x] = 1, then {x} = 2/3
Thus, x = [x] + {x} = 1 + 2/3 = 5/3
If [x] = 0, {x} = 0
x = 0
Solutions   x {0, 5/3}


Q.6. Find range for y = .

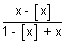
Ans:   y = =
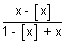
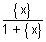
Domain R
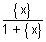
y =   {x} =
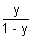
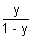
Since   0 {x} < 1   0 < 1   0 y < 1/2

range = (0, 1/2)


Q.7. Let f(x) be periodic & k bca +ve real no. such that f(x + k) + f(x) = 0 v x R. Prove that f(x) f(x) is periodic with period 2k.

Ans: f(x + k) + f(x) = 0 v x R
       f(x + k) = - f(x) v x R ................................................... (i)
put   x = x + k
f(x + 2k) = -f(x + k) v x R
from (i)
    f(x + 2k) = f(x), v x R
  f(x) is peruiodic with period 2k.


Q.8. Find period of f(x) = tan3x + sin

Ans: Period for tan 3x is
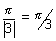
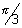
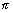
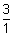
Period for sin   is |2 x = 6
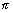
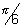
 LCM of sin^-1 <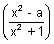
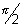
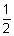
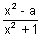
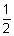
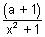
< 1   1 - < 1, v x R
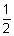
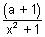
- - < 0
a + 1 > 0
a (-1, )


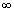
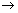
Q.10. If f : R R   f(x) = x² + 1, then find value of f^-1(17).

Ans: f(x) = x² + 1
       f^-1(17)   f(x) = 17
   x² + 1 = 17   x = ±4
       x = {4, -4}




Q.1. Find domain of function. f(x) =

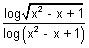
Ans: log(x² - x + 1) is defined when
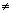
    x² - x + 1 > 0   &   x² - x + 1 1
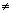
x R   and   x 0, 1
x R - {0, 1} ..................................... (i)

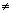
[Dumb Question: How x² - x + 1 > 0 v x R & why x² - x + 1 1 ?
  Ans: ax² + bx + c > 0 v x R if a > 0 & D < 0
For x² - x + 1, a = 1 > 0 & D = 1 - 4 = - 3 < 0
So, x² - x + 1 > 0 for all x R
& If x² - x + 1 = 1 then logx² - x + 1 = 0
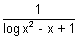
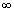
& = which is not desired.]

Again log(sin^-1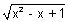) exists when x² + x + 1 > 0 & x² + x + 1 1
i.e.   0 < x² + x + 1 1
x² + x 0   x [-1, 0] .............................. (ii)
From (i) & (ii)
x [-1, 0)


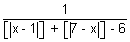
Q.2. Find domain of f(x) =   where {} is greatest integer function.

Ans: f(x) is defined when
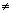
    [|x - 1|] + [|7 - x|] - 6 0

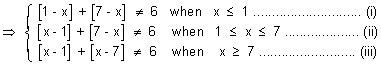
Taking (i)
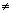
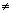
    [1 - x] + [7 - x] 6   1 + [-x] + 7 + [-x] 6
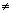
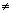
2[-x] - 2   [-x] - 1
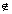
x (0, 1] ................................... (1)
From (ii)
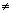
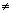
    [x - 1] + [7 - x] 6   [x] - 1 + 7 + [-x] 6
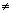
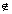
[x] + [-x] 0   x Integer
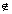
x {1, 1, 3, 4, 5, 6, 7} ................. (2)
From (iii)
    x [7, 8) ..................................... (3)
From (1), (2) & (3)
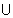
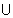
Domain f(x) R - {(0, 1] {1, 2, 3, 4, 5, 6, 7} [7, 8)}


Q.3. f(x, y) is periodic function satisfying condition f(x, y) = f((2x + 2y),(2y - 2x)) v x,y R. Now g(x) = f(2^x, 0) then prove that g(x) is periodic function, find its period.

Ans: f(x, y) = f(2x + 2y, 2y - 2x) ....................................... (i)
Put x = 2x + 2y & y = 2y - 2x
f(2x + 2y, 2y - 2x) = f(2(2x + 2y) + 2(2y - 2x), 2(2y - 2x) - 2(2x + 2y))    [By (i)]
f(x, y) = f(2x + 2y, 2y - 2x) = f(8y, - 8x)
f(x, y) = f(8y, - 8x) ..................................................... (ii)
f(8y, - 8x) = f{8(- 8x), - 8(8y)}    [By (ii)]
f(x, y) = f(2x + 2y, 2y - 2x) = f(8y, - 8x) = f(- 64x, - 64y)
f(x, y) = f(- 64x, - 64y) ............................................... (iii)
f(- 64x, - 64y) = f(64 x 64 x, 64 x 64y) = f(2¹²x, 2¹²y)    [By (iii)]
f(x, y) = f(2¹²x, 2¹²y)
f(2^x, 0) = f(2¹².2^x, 0) = f(2^{12 + x}, 0)
g(x, 0) = f(2^x, 0) = f(2^{12 + x}, 0)
g(x, 0) = g(x + 12, 0)
g(x) is periodic with period


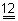
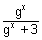
Q.4. Let f(x) = . Show that f(x) + f(1 - x) = 1 & hence, evaluate


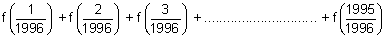
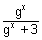
Ans: f(x) = ................................................. (i)
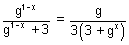
and  f(1 - x) = .............................. (ii)
Adding (i) & (ii), we get
   f(x) + f(1 - x) = +
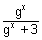
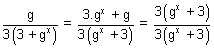
f(x) + f(1 - x) = 1 ............................................. (iii)
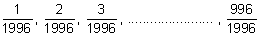
Now, putting   x = in (iii).

........................
........................
........................
........................
........................
........................

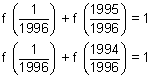
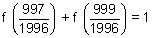
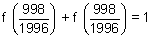
  or  
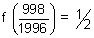
Adding all.


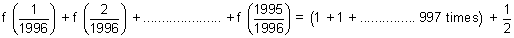
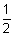
[Dumb Question: For what is added ?
  Ans: For ]

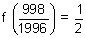
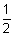
   = 997 + = 997.5


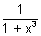
Q.5. Let g(x) be inverse of f(x) and f'(x) = . Then find g'(x) in terms of g(x).

Ans: Since g(x) is inverse of f(x)
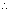
  (gof)(x) = x
g{f(x)} = x
g'{f(x)} f'(x) = 1
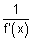
g'{f(x)} = = 1 + x³
g'{f(g(x))} = 1 + (g(x))³
g'(x) = 1 + (g(x))³


Dumb Question: How f(g(x)) = x ?

Ans: Since g(x) is inverse of f(x)
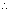
f(x) is also inverse of g(x)
By inverse property
f(g(x)) = x