Gas Laws - 2
(c) Avogardo’s Law: Equal volume of all gases under same conditions of temperature & pressure contain equal no of molecules.
V = Kn But n = 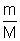 (m = mass, M = Molar gas)
(m = mass, M = Molar gas) V =
V = 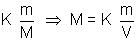 = Kd d
= Kd d 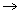 density
density
=> density of gas is directly proportional to its molar mass.
M 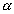 d d |
III. Ideal Gas Equation:
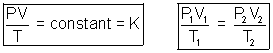
Volume of constant K depends only upon amount of gas taken. If n is no. of moles of gas taken.
K 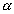 n n |
| K = nR |
R
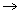 Universal gas constant.
Universal gas constant.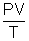 = nR
= nRPV = nRT
 Ideal Equation.
Ideal Equation.Derivation:
According to Boyles law
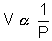 at constant T ................................................................ (1)
at constant T ................................................................ (1)According Charle's law
V
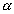 T at constant P ................................................................ (2)
T at constant P ................................................................ (2)According to Avogardo's law
V
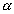 n at constant T & P ................................................................ (3)
n at constant T & P ................................................................ (3)Combing (1), (2) & (3)
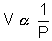 x T x n
x T x n=> PV = nRT K
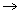 .......
.......Ideal Gas Equation (in terms of density):
If M is mass of gas in gm & M is molar mass of gas, then
n =
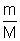
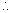 PV =
PV = 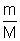 RT =
RT =  RT
RTP =
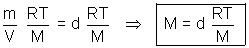
Volume of Gas constant (R):
R =
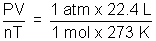 = 0.082 L atm K-1 mol-1
= 0.082 L atm K-1 mol-1In SI unit
R = 8.314 J K-1 mol-1
In terms of calori e
R =
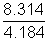 = 1.987 Cal K-1 mol-1>
= 1.987 Cal K-1 mol-1>Illustration: Temperature at foot of mountain is 300C & pressure is 760 mm whereas at top of mountain there are 00C & 710 mm. Compose densities at top & bottom of mountain.
Ans: d =
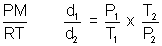
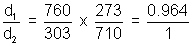
If two or more unreaching gases are enclosed in a vessel, total pressure exerted by gaseous mixture is equal to sum of all partial pressures that eact gas would exert when present alone in same vessel at vessel temperature.
| P = P1 + P2 + P3 + .................. + Pn |
Applications:
(i) In determination of pressure of dry gas e:
| Pdry gas = Pmoist gas - Aqueous tension |
Dumb Question: What is equation tension ?
Ans: Pressure exerted by water vapours in moist gas.
(ii) In calculation of partial pressure:
PV = nRT
PA = nB
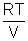 PB = nB
PB = nB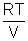
PA & PB
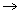 Partial pressure.
Partial pressure.By Dalton's law
Total pressure, P = PA + PB + PC + ...................
=
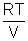 (nA + nB + nC + ..................)
(nA + nB + nC + ..................)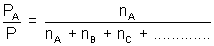 = xA(mol.Fraction of A)
= xA(mol.Fraction of A)| PA = = P x xA |
Question: 270C & 746.5 mm pressure. Calculate volume of gas at 00C & 760 mm pressure (Aq. tension at 270C is 26.5 mm).
Ans:
[Dumb question: Why there is no ag. tension at 00C ?
Ans: At 00C, there is no water vapours. So, no, ag. tension at 00C.]
Initial Condition Final condition
V1 = 38 ml V2 = ?
P1 = 746.5 - 26.5 P2 = 760 mm
= 720 mm
T1 = 27 + 273 = 300 K T2 = 0 + 273 = 273 K
By gas equation
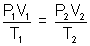
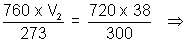 V2 = 32.76 ml.
V2 = 32.76 ml.Illustration: A gaseous mix contains 56g N2, 44g CO2 & 16g CH4. Total pressure of mix is 720 mm Hq. What is partial pressure of CH4 ?
Ans: nN2 = 56/28 = 2 nCO2 = 44/44 = 1
nCH4 = 16/16 = 1
nTotal = 2 + 1 + 1 = 4
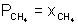 x Total pressure
x Total pressure= 1/4 x 720 = 180 mm.
Diffusion: Spreading of molecules of a gas throughout available space.
Sffusion: In this process gas under pressure escapes out of fine hole.
At constant temperature & pressure, rates of diffusion of different gases are inversely proportional to square root of their densities.
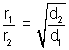
Rate of diffusion/effusion =
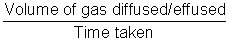
| Mol. Mass = 2 x V.P. |
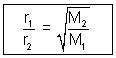
Note: If pressure is different of two gases then greater pressure, greater is no. of molecules hitting per unit area, greater is rate of diffusion.
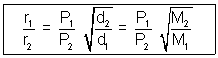
r1 = v1/t r2 = v2/t
v1
 Volume diffused of I gas.
Volume diffused of I gas.v2
 Volume diffused of II gas.
Volume diffused of II gas.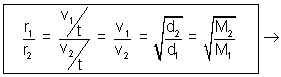 Time ia constant for two gases.
Time ia constant for two gases.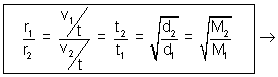 Volume of two gases is constant.
Volume of two gases is constant.Question: 200 c,, HCl gas & NH3 are allowed to enter. At what distance NH4Cl will Ist appear ?
Ans: By Graham's law of diffusion
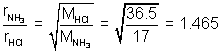
Thus, NH3 travels 1.465 times faster than HCl.
In other words. Since area of x-section is square, NH3 will travel 1.465 cm in same time in which HCl travel 1 cm.
Length of tube = 200 cm
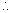 Distance travelled in tube by NH3 =
Distance travelled in tube by NH3 = 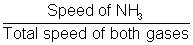 x Total distance
x Total distance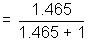 x 200 = 118.9 cm
x 200 = 118.9 cmSo, NH4Cl will Ist appear at distance of 118.9 cm from NH3 and or 81.1 cm from HCl end.