Gas Laws - 6

Question: & 0.0566 L mol. Calculate a, b & R
Ans: Given T_C = 374 + 273 = 647 K, P_C = 218 atm
V_C = 0.0566 L mol^-1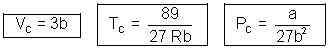


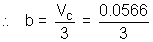= 0.0189 L mol^-1
    a = 3P_CV_C² = 3 x 218 x (0.0566)² = 2.095 L² atm mol^-2
    R = 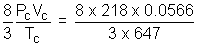= 0.05086 L atm K^-1mol^-1

Medium Type:

Q1. A large flask filled with stop cock is evacuated & weight its mass is found to be 134.567 g. It is then filled to pressure 735 mm at 31⁰C with a gas of unknown molecular mass & then reweighed; its mass is 137.456 g. Flask is then filled with H₂O & weighed again, its mass is now 1067.9 gm. Calculate molar mass of gas if gas is ideal.
Ans: Mass of meter filling flask = (1067.9 - 134.567)g
                                            = 933.333 g
Volume of flask = Volume of meter = 933.333 ml

Dumb Quetion: Why volume of meter is 933.333 ml ?
Ans: Because density of meter is 1 g/cm³
P = 735 mm,    T = 273 + 31 = 304 K,    V = 933.33
By PV = nRT

    n = 0.036 mol
Mass of 0.036 mol of gas = (137.456 - 134.567) g
                                    = 2.889 g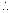
Mass of 1 mol of gas = 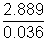= 80.25 g

Q2. Avg. speed at T₁K & Most probable speed at T₂K of CO₂ gas is 9 x 10₄ cm/s. Calculate value of T₁ & T₂.
Ans: Avg. speed = 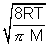   Most probable speed =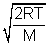
Avg. speed at T₁K = MP speed at T₂K for CO₂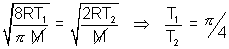
……………………………….. (i)
For CO₂ U_mP = 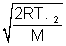= 9 x 10⁴
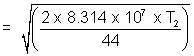                  = 9 x 10⁴
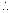T₂ = 2143.37 K
By eq. (i) T₁ = 1684 K

Q3. Mass of molecule A is twice mass of molecule B. RMS speed of A is twice rms speed of B. If two samples of A & B contains same no. molecules. What will be ratio of P of two samples in separate containes of equal volume.
Ans: Given, m_A = 2m_B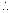

Mol. wt. of A = 2 x Mol. wt. of B

Given U_rms of A = 2 U_rms of B

For gas A      P_AV_A = 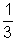M_A u²_{rms A}
Fr gas B      P_BV_B = 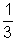M_B u²_{rms B}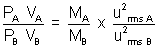

Given V_A = V_B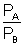
= 2 x (2)² = 8

PA = 8 PB

Q4. One way of writing eq. of state of writing eq. of state of real gases is PV = RT[1 + B/V + ..........] where B is constant. Derive expression for B in terms of Vander Waal's constant a & b ?
Ans: According to Vander Waal's Equation
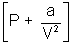    [V - b] = RT
    P =
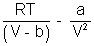
Multiply by V
    PV =
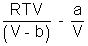
    PV = RT
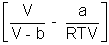
    PV = RT

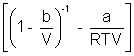
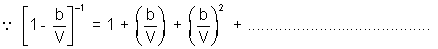
    PV = RT
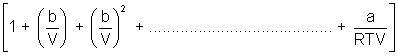
On comparing



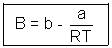
Q5. A glass capillary tube scaled at both ends is 100 cm long. It lies horizontally with middle 10 cm containing Hg. Two ends are equal in length contain air at 27⁰C & pressure > 6 cm od Hg. Tube is kept in horizontal position, the one end is at 0⁰C & other end is at 127⁰C. Calculate length of air column & pressure which is at 0⁰C.
Ans:

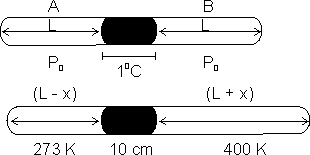
     2 L + 10 = 100
=> L = 45 cm
Let initial pressure be P_o atm on each side. When one end is cooled & other heated, expansion of gas takes place at hoter end till pressure of two sides becomes same.
i.e. P₁ = P₂ = P
For end A. 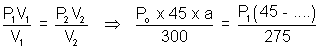   .......................... (i)
a 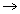area of x - section of tube.
For end B, 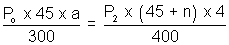   ................................. (ii)
Equating.     P₁ = P₂

                 
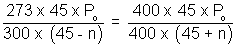
                 x = 8.49 cm
                 P₁ = 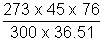= 82.25 cm of Hg

Hard Question:

Q. An LPG cylinder weighs 14.8 Kg when empty, when full, it weighs 29 Kg & shows pressure of 2.5 atm. During use at 27⁰C weight of full cylinder reduced to 23.2 Kg. Fid out volume of gas in m³ used up at normal condition & final pressure inside cylinde. Assume LPG to be n-butane.
Ans: Wt: of butane in cylinder = 29 - 14.8 = 14.2 Kg = 14.2 x 10³
P = 2.5 atm, T = 300 K, Mol. wt. of butane = 58
PV = 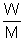RT
2.5 x V = 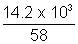x 0.0821 x 300
V = 2.4 x 10³ L = 2.4 m³
Now, wt. of as left after use = 23.2 - 14.8 = 8.4 x 1³ g
Volume remains constant
PV = RT
P x 2.4 x 10³ = 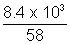x 0.0821 x 300
wt. of gas given out = 29 - 23.2 = 5.8 Kg
                             = 5.8 x 10³ g
Volume of gas given out
    1 x V = x 0.0821 x 300
V = 2.4 x 10³ L = 2.4 m³