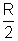Geometric Optics - 1 · KnowledgeBin.org

Introduction

OPTICS is study of propagation of light. In Geometric optics we are just concerned about, what the path of light is when it gets reflected or refracted. While dealing with Geometric optics we consider light rays to e paraxial i.e. which re very near to each other and thus a lot of assumptions could be encorprarted. In this unit we answer why a coin placed in water appear to be little bit raised above and many such phenomenom.

REFLECION:

When a ray of light is incident at a point on the surface, the surface throus party or whally the incident energy back into the medium of incidence. This phanomenon is called reflection.
Surface that causes reflection are known as mirrors or reflectors.

Important terms related to reflection:

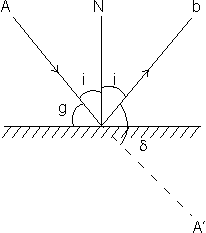
Angle of incidence: Angle which the incident ray makes with the normal at the point of incidence. (densted i)

Angle of reflection: The angle which the reflected ray makes with the plane normal of the point of incidence. (densted by r)

Glancing Angle: The angle which the incident ray makes with the plane reflecting surface is called glancin angle. It is generally denoted by g.
g = 90 - i

LAWS OF REFLECTION:

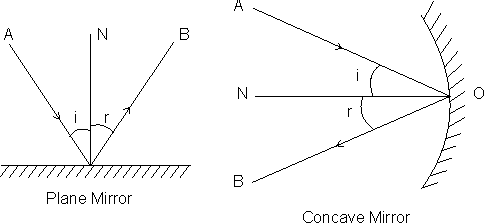
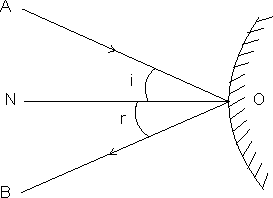
(i) The incident ray, the reflected ray and the normal to the reflected surface at the point of incidence lie in same plane.

(ii) The angle of incidence is equal to the angle reflection, i.e. i = r. These laws hold for all reflecting surfaces either plane or crowed.

Dumb Question: Do incident ray and reflected ray differ in terms offrequency, wavelength and speed ?

Ans: None of frequency, wavelength and speed changes due to reflection. However, intensity and have amplitude (I

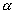A²) usually decreases. However in ray optics we do not consider this change.

Dumb Question: What will happen if incident ray falls along Normal to the surface ?

Ans: In what case i = 0 so r = i = 0

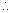it will retrace its path.

Dumb Question: How do we determine the 'Normal' in case of spherical surface ?

Ans: Spherical surfaces are a part of circle. So Normal at a point on the surface is the line joining that point with the centre of circle (of which the mirror is a part).

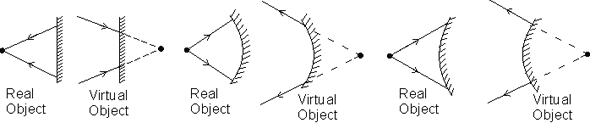
IMAGE FORMATION: Image is said to the formed when two rays meet. The image can be real or virtual.

Real Image: If the rays actually at a point then the image formed is regarded as real image.

Virtual image: If the reflected or refracted rays do not actually meet out only appear to diverge from the point, then it is said that a virtual image is formed at that point.

Dumb Question: Just as we have real and virtual image, do we have real and virtual objects too ?

Ans: Object is a point from where rays diverge. If the rays actually start from a point then that is called real object. If however the rays appear to be starting from a point than that object is regarded as virtual object.

Characteristics of the image formed by o plane mirror:

(i) The image formed is atthe same distance behind the reflecting surface as the object is in front of it.

(ii) The size of the image is the same as that of the object.

(iii) The image is virtual and erect which means no light passes through it.

(iv) The image is laterally inverted. i.e. side-wise inverted.

Dumb Question: What is the meaning of 'side-wise inverted' ?

Ans: The image of right hand appears identical to left hand in a mirror. This is 'side-wise inverted'.

Illustration: Two plane mirrors are indined at angle

with each other. A ray strikes one of them. Find its deviation after it has reflected twice-one from each mirror.

Solution: Case I:

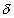₁ = Clockwise deviation at A = 180 - 2i₁

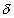₂ = Anticlockwise deviation at B = 180 - 2i₂
Now from

OAB, we have
angle O + angle A + angle B = 180⁰
=> i₁ - i₂ =

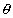
as i₁ > i₂,

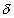₁ <

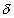₂
Hence the net angle clockwise deviation =

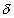₁ -

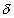₂
= (180 - 2i₂) - (180 - 2i₁)
= 2(i₁ - i₂) = 2

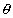
Case II:

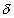₁ = Clockwise deviation at A = 180 - 2i₁

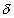₂ = clockwise deviation at B = 180 - 2i₂
Now from

OAB, we have
angle O + angle A + angle B = 180⁰
or

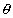+ (90 - i₁) + (90 - i₂) = 180⁰
=> i₁ + i₂ =

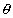
Hence, net clockwise deviation =

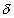₂ +

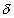₁
= (180⁰ - 2i₂) + (180⁰ - 2i₁)
= 360 - 2(i₁ + i₂) = 360 - 2

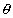
=> Net anti-clockwise deviation = 360⁰ - (360⁰ 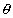- 2

) = 2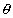

Dumb Question: What is deviation and how it is calculated ?

Ans: Deviation is defined as the angle between direction of the incident ray and the reflected ray. It is denoted by

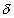Here

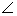A'OB =

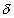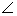AOA' -

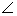AOB
= 180⁰ - 2i
We know g = 90 - i

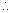
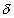= 2g

• If two mirror are kept inclined to each-other at angle

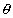with their reflecting surfaces facing each-other, then multiple reflections take place and more than are images are formed.
Number of images formed n =

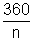- 1 [if

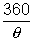is on even integer]

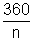[if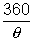

is on odd integer]

• Rotation of the reflected ray by a mirror: Keeping the incident ray fixed, if the plane mirror is rotated through an angle

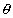about an axis in the plane of mirror, then the reflected ray is rotatde through an angle 2

.
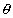How ??

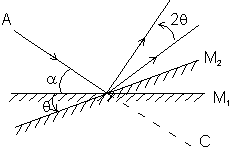
The glancing angle with M₂ = (

)
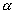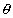Hence, the new angle of deviation (i.e.

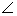COP) = 2(

)
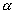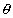The reflected ray has thus been rotated through

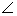BOP when the mirror is rotated through an angle

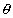and since

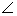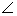BOP =

COP -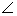

COB or

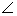BOP 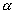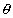= 2(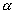

) - 2

= 2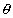

SPHERICAL MIRRORS:

Some important definition:

• Spherical mirrors are a part of a hollow sphere or spherical surface. They can be concave or convex.

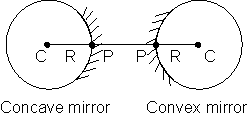
• POLE OR VERTEX: It is the geometrical center of the spherical mirror (P in this case)

• RADIUS OF CURVATURE (R): Radius of curvature is the radius R of the sphere of which the mirror forms a part.

• PRINCIPAL AXIS: The line CP joining the pole and the centre of curvature of the spherical mirror is called the principal axis.

• FOCUS (F): If a parallel beam of rays, parallel to the principal axis and close to it, is incident on a spherical mirror, thereflected rays converge to a point F (in case of a concave mirror) or appear to diverge from a point F (in case of a convex mirror) on the principal axis. The point F is called the focus of the spherical mirror.

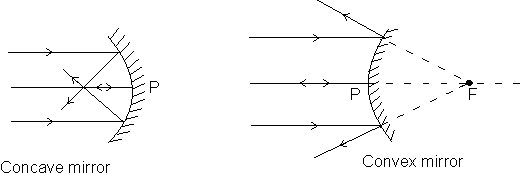
• Focal length (f): Focal length is the distance PF between the pole and focus F along the principle axis.

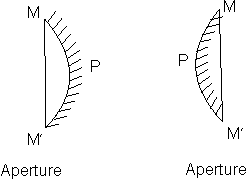
• Aperture: The line joining the end points of a spherical mirror is called the aperture or linear aperture.

RELATION BETWEEN f AND R:

The magnitude of focal length in spherical mirrors in half the radius of curvature i.e.
f =

Related Guides