Geometric Optics - 2
RULES FOR IMAGE FORMATION:
(i) A ray parallel to principal axis passes (or appear to pass) through focus after reflection.
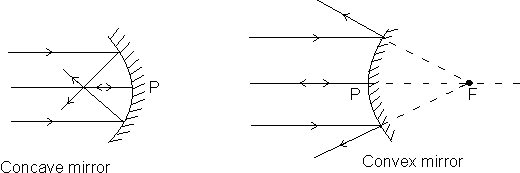
(ii) A ray passing through or directed towards focus after reflection from the spherical mirror becomes parallel to the principal axis.
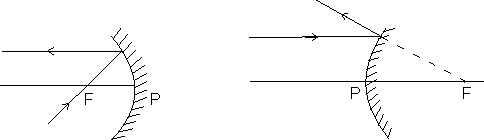
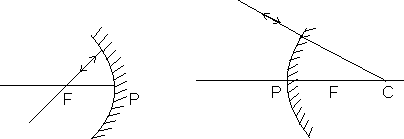
(iii) A ray passing through or directed towards the centre of curvature, after reflection from the spherical mirror, retroces its path (see dumb question).
Dumb question: How do 4 use these rules and where to apply them ?
Ans: These rules are to be used for making the ray diagram and find the nature of image. For image formation, we need two rays. So choose one ray to be the one parallel to the principal axis and passing through the object. Apply Rule (ii) for trcking rest of path. Other ray can be choosen as the one which comes from focus .
Image formation by cancave mirror
| Position of object | Nature of image | Position |
| (i) infinity | real, inverted, highly diminished | at F |
| (ii) beyond C | real, inverted and diminished | between F & C |
| (iii) at C | real, inverted, same size | at C |
| (iv) between F and C | real inveted and enlarged | beyond C |
| (v) at F | real, inverted, highly enlarged | at  |
SIGN CONVENTION:
The pole is taken as the origin and rest of the distances are calculated according to it. Thus
• All the distances on the right side are +ve. Thus focus is +ve in case of convex mirror while it is -ve in case of concave mirror.
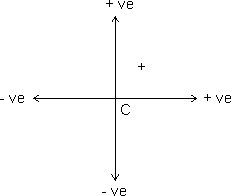
• Above rule holds, if incident ray is travelling from left to right else directions just reverses.
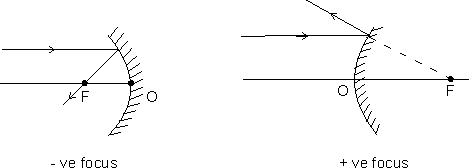
• Distances measured above principal axis are taken to be positive while distances measured below principal axis are taken to be negative.
notations used:-
u:
Distance of the object from pole of spherical mirror.v:
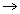distance of the image from the pole of the spherical mirror.f:
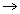focal length of the spherical mirror.R:
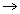Radius of curvature of the spherical mirror.• All the symbols used are assigned values with proper sign convention. i.e. for concave mirror f is always -ve and so on.
MIRROR FORMULA:
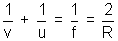All values have to placed in the equation with proper sign.Dumb Question: Is the above formula valid for simple mirror also ?
Ans: This is a general formula for all spherical mirror. For flat mirrors R =
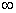, as it can be assumed to be a part of sphere with infinite radius, then this equation can be used. It yeilds
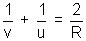= 0 => v = - u which correctly describes image formation in a flat mirror.
LINER MAGNIFICATION:
For linear objects, the ratio of the image size (I) to the object size (O) is called linear magnification or transverse magnification or lateral magnification. If is generally denoted by m.
m =
m =
Illustration: A plane mirror is placed 22.5 cm in front of a concave mirror of focal length 10 cm. Find where an object can be placed between the two mirrors, so that the first image in both the mirrors coincides.
Solution:
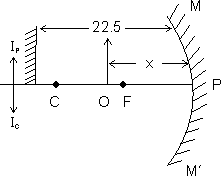
As shown in figure, if the object is placed at a distance x from the concave mirror, its distance from the place mirror will be (212.5 - x). So, plane mirror will form equal and erect emage of object at a distance (22.5 - x) behind the mirror.
Now as according to given problem the image formed by concave mirror coicides with the image formed by concave mirror, therefore for cancave mirror
v = - [22.5 + (22.5 - x)] = - (45 - x) and u = - x
So,
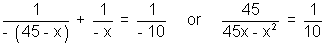
i.e. x2 - 45x + 450 = 0 or (x - 30)(x - 15) = 0
i.e. x = 30 cm or x = 15 cm
But as the distance between two mirrors is 22.5 cm, x = 30 cm is not admissible. So the object must be at a distance of 15 cm from concave mirror.
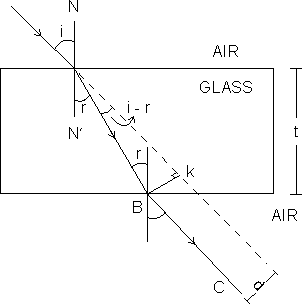
REFRACTION:
Whenever a ray of light from one transparent medium to another, it gets deviated from its original path while crossing the interface of the two media (except in case of normal incidence). This phenmenon of devition or bending of light rays from their original path while passing from one medium toanother is called refraction.
AB
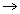incident ray BC refracted ray NBN' Normal i
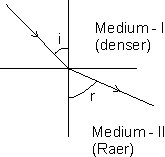
angle of incidence r angle f refraction KL interface • If the refracted ray bends towards the normal with respect to the incident ray, then the second medium is said to be optically denser as compared to the first medium.
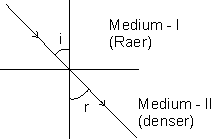
• If the refracted ray bends away from the normal, then the second medium is said to be (optically) as compared to the first medium.
LAWS OF REFRACTION:
(i) The incident ray, there fracted ray and the normal to the refracting surface at the point of incidence, all lie in the same plane.
(ii)The ratio of sine of the angle of incidence to the sine of the angle of refraction is constant for any two given media
i.e.
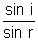= constant = 1µ2 = Refractive index.This is called Snell's law.
Refractive index:
• 1µ2 =
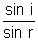then 1µ2 (or 1n2) is a constant called refractive index of the second medium w.r.t. first medium (containing incident ray)• 1µ2 =
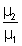where µ2 is absolute refractive index of second medium and µ1 is of first.• Refractive index is a relative quantity. If the first medium is air (vaccum to be precise) then
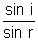= µ or n called absolute refractive index.
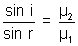=> µ1 sin i = µ2 sin r = constant.product of absolute R % of medium and sine of rays with normal in that medium is constant.
Dumb Question: What actually occurs in the process of refraction and what is true significances of µ ?
Ans: During refraction, the velocity of light changes at the interface and thus light follows an alternative path.
µ is actually ratio of light in vaccum with the speed of light in given medium
µ 1µ2 =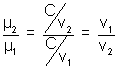 
Dumb Question: What parameter of wave changes during refraction.
Ans: During the process of refraction only frequency of light remains constant, while wavelength and velocity change
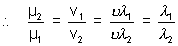
Dumb Question: What is the meaning of 'rare' and 'dense' when associated with medium ?
Ans: 'rare' and 'dense' are also relative terms. When compared the medium with higher value of refractive index is called 'denser medium' and the other one is called rarer medium.
Dense medium is the one in which light travels slower than in rarer medium.
LATERAL DEVIATION (through a glass slas):
