Geometric Optics - 3
If there exists a region of index through which ray has to pass; such that there exists a medium of same refractive index on the entry and exit of the ray then the ray gets laterally shifted by distance d
d =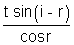 
    where t 
length of region
Why ??
In wright angled 
OBK,    we have     
BOK = i - r
sin(i - r) =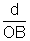 
            or             d = OB sin(i - r) …………………………… (i)
In right angled triangle ON’B, we have
cos r =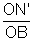 
    or     OB =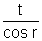 
Substituting the above of OB in equation (i), we get
d = 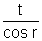sin(i - r)
Dumd Question: In the adjacant system what is the angle between incident ray and emergent ray ?
Ans:
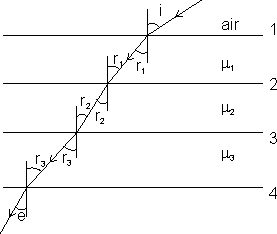
Applying Snell's law at first interface
sin i = sin r1 ............................................. (i)
Applying Snell's law at 2, 3 & 4
We get
µ1 sin r1 = µ2 sin r2 .................................... (ii)
µ2 sin r2 = µ3 sin r3 .................................... (iii)
µ3 sin r3 = sin e ......................................... (iv)
Combining all the form equation we get
sin i = µ1 sin r1 = µ2 sin r2 = µ3 sin r3 = sin e
or sin i = sin e
=> i = e
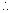emergent ray is parallel to incident ray. This result is independent of no. of slabs used and holds as long as incident ray and emergent ray are in same medium.Apparent depth:
When the object is in different medium and observer is in different medium, then the object seems to be
(i) nearer to the observer (if object is in denser o medium).
or
(ii) farther to the observer (if object is in rarer medium).
Then the actual depth
Apparent depth =
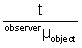
where µ is refrective index of object medium w.r.t. that of observer's medium.
for case (i) the apparent shift is given by t -
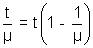
Why ??
In the above figure
sin i
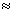tan i = 
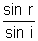II'ly sin r 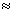tan r =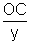 
(the approxiamation holds because i & r are small angles)
from Snell's law
µ =
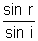=> µ =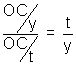 
=> y =
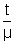
Similarly the other case can be proved (when object medium is rarer)
Dumb Question: Whar will happen if a glass slab of thickness 't' is placed between object and a mirror.
Ans:
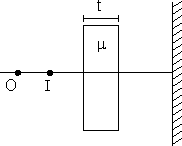
In that case, the point of intersection of ray shifts by t(1 - 1/µ) in the direction in which the ray is moving.
(where µ is refractive index of glass slab) And calculation needs to be made according to this new position.
Illustration: A fish rising vertically to the surface of water in a lake uniformly at the rate of 3 m/s observes 9 m/s vertically above it. If the refractive index of water is 4/3 find the actual velocity of the dive of the bird.
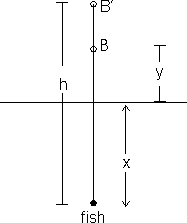
Solution: If at any instant the fish is at the depth 'x' below fish water surface while the bird at a height y above the surface, then the apparent height of the bird from the surface as seen by the fish will be given by
µ =
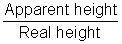or Apparent height = µySo, the total apparent distance of the bird as seen by the fish in water will be
h = x + µy
or
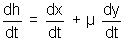or 9 = 3 + µ(
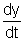)or
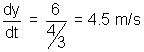
CRITICAL ANGLE & TOTAL INTERNAL REFLECTION:
• When a ray of light goes from adenser medium to a rarer medium, the angle of refraction is greater than the angle of incidence. If the angle of incidence is increased, the angle of refraction may enentually become 900.
• This incidence angle is called critical angle (C).
• If the angle is increased furthe, then the ray comes back in the medium of incidence. This phenomenon is called total INTERNAL REFLECTION.
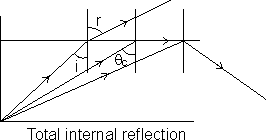
• Crtical angle is sin C =
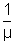where µ =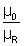 
Dumb Question: Is Snell's law applicable for total internal reflection ?
Ans: Snell's law no more holds for total internal reflection, however we can apply laws of Reflection to totally internally reflected ray.
Illustration: A ray of light from a denser medium strikes a rarer medium at an angle of incidence i If the reflected and the refracted rays are mutually perpendicular to each other, what is the value of the critical angle ?
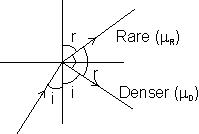
Solution: From Snell's law, we have
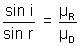
or µ =
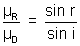........................................ (i)According to the given problem i + r 90 = 180
or r = 90 - i
Substituting the above value of r in equation (i), we get
µ =
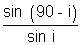
or µ = cot i ................................................ (ii)
By definition
C = sin-1(
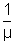) or C = sin-1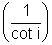
Using equation (ii)
or C = sin-1(tan i)
REFRACTION THROUGH PRISM:
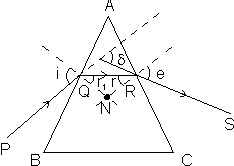
If A is the angle of prism,
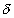deviation caused due to it, i, angle of incidence and e angle of emergence than 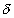+ A = i + e Why ??
In the quadrilateral AQNR, two of the angle (at the verticles Q and R) are right angle. Therefore, the sum of the other angles of the quadrilateral is 1800.
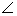A + 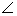QNR = 1800 from the triangles QNR, r1 + r2 + 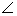QNR = 1800Comparing these two equations, we get r1 + r2 = A
The total deviation
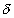is the sum of deviations at the two faces: 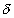= (i - r1) + (e - r2) = (i + e) - (r1 + r2) =>
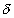= (i + e) - A =>
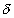+ A = i + e Dumb Question: For same prism do e have some deviation for all rays ?
Ans: At the two interface, applying Snell's law we have
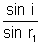= µ and 
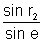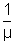
= deviation depends upon the refraction index, which further is depend upon wavelength ray. Thus deviation is different for rays of different wavelengths.
Dumb Question: Can we have same deviation for more than one angle of incidence ?
Ans: It can be easily seen that if we reverse the emergent ray, it goes back along the same path. The angles of incidence and emergence get interchanged but the angle of deviation remains the same.
Thus the same angle of deviation
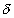is possible for two different angles of incidence: i and e such that i + e = A +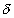 Illustration: A ray of light is incident on one face of a prism (µ = 1.5) at an angle of 600. The refracting angle of the prism is also 600. Find the angle of emergence and the angle of deviation. Is there any other angle of incidence which will produce the same deviation ?
Solution:
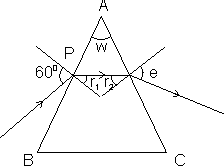
Angle of incidence = i = 600
at point P,
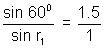
=> sin r1 =
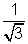
or r1
3506' using r1 + r2 = A At point Q,
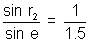=> sin e = 1.5 sin 24044 sin e = 0.63
=> e = 390
Deviation = 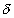= (i + e) - A = (60 + 39) - (60) = 390 If i and e are interchanged, deviation remains the same. These same deviation is obtained for angles of incidence 600 and 390.
Dumb Question: What will happen if the angle of the prism is greater than twice the critical angle for the material of the prism ?
Ans: We know r1 + r2 = A > 2C or r1 + r2 > 2C
these occurs two cases:
(i) r2 > C the ray not go out of prism. rather will be reflected back inside. This is physically not possible as in that case incident ray.
(ii) r1 > C this is physically not possible as in that case incident ray couldn't have entered the prism.
These occurs third case too r1 > C & r2 > C here also result of (ii) will hold.
MINIMUM DEVIATION:
Adjacant figure shows the experimental plot of
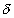Vs i graph for a prism.
for this case i = e and r1 = r2
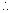The equation modifies as 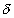+ A = i + e = 2i or i =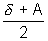 
II'ly r1 + r2 = A or r1 = A/2
Applying Snell's law for first surface, the equation yields
µ =
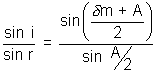[Refraction index of prisom] for prism of small angle (< 100) we have approximations for sin e
µ =
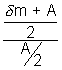=> µ =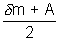 
or
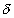m = (µ - 1)A