Geometric Optics - 4

FEW IMPORTANT TERMS:

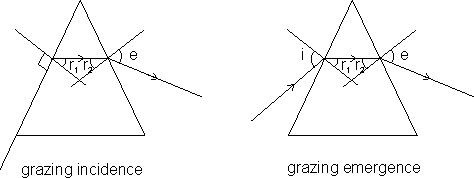
• Grazing Incident: When i = 90⁰, in this angle of refraction becomes equal to critical angle.

• Grazing Emergence: When e = 90⁰, here   r₂ = Critical angle.

• Maximum Deviation: We know   = (i + e) - A
deviation will be maximum when the angle of incidence i is maximum i.e. i = 90⁰.
Here,
()_max = (90⁰ + e) - A      expression for maximum deviation.


Illustration: Find the manimum and maximum angle of deviation for a prism with angle A = 60⁰ and µ = 1.5.

Solution: Minimum deviation:
The angle of minimum deviation occurs when i = e and r₁ = r₂ and is given by
µ = 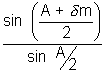    =>   _m = 2 sin^-1(µ sin A/2) - A
Substituting   µ = 1.5 and A = 60⁰, we get
_m = 2 sin^-1(0.75) - 60⁰ = 37⁰


Maximum Deviation:
The deviation is maximum when i = 90⁰ or e = 90⁰ that is at grazing incidence or grazing emergence.
Let i = 90⁰
=> r₁ = C = sin^-1(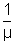)     => r₂ = sin^-1(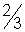) = 42⁰
=> r₂ = A - r₁ = 60⁰ - 42⁰ = 18⁰
Using 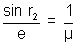   , we have
=> sin e = µ sin r₂ = 1.5 x sin 18⁰ = 4.63
=> e = 28⁰
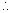Deviation = _max = (i + e) - A = (90⁰ + 28⁰) - 60⁰ = 58⁰


DISPERSION OF LIGHT THROUGH PRISM:

When a ray of white light is passed through a prism, it spits up into its constituent colours. This phenomenon of splitting up of white light into constituent colours is called DISPERSION.

• Cauchy's expression forrefractive index   µ = a + 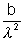   a,b -> Constant of material.
Since each colour has different wavelength hence refractive index will be different for different colours.

ANGULAR DISPERSION: 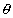   = _V - _R = (µ_V - µ_R)A
it is the angle between the extreme rays of dispassed colour band, which are violet and Red.



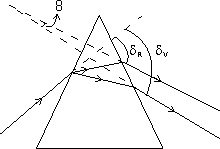
DISPERSIVE POWER (W): The ratio of (angular) dispersion to the deviation of the mean ray (yellow) is called the dispersive power of the prism. It is denoted by W.
W = 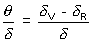, where is the deviation of the mean ray
In term of refractive index
W = 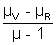,    where   µ =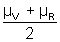


Illustration: Calculate the diapersive power of crown and flint glass-prism from the following data: for crown glass                        for crown glass
µ_V = 1.522; µ_R = 1.514                                   µ_V = 1.662; µ_R = 1.644

Solution: For crown glass      µ_V = 1.522; µ_R = 1.514
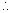µ_y = 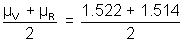= 1.518
Hence, the dispersive power of crown glass
W = 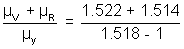= 0.01544
for flint glass    µ_V = 1.662; µ_R = 1.644
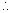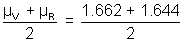µ = = 1.6


DISPERSION WITHOUT DEVIATION:


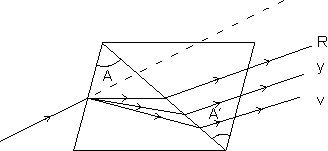
Let two prisms of angle A & A' be placed as shown in figure. If the system produces net deviation as zero
then 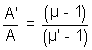       where µ & µ' are the refractive index of mean wavelength.


Dumb Question: What is the meaning of 'dispersion without deviation' ?

Ans: The rays gets dispersed, however, the mean ray remains parallel to the incident ray, i.e. angle between incident and mean emergent ray is zero.
Condition for it os + ' = 0   or   (µ - 1)A + (µ' - 1)A' = 0
this yields the required result.


DEVIATION WITHOUT DISPERSION (ARCHROMATIC COMBINATION OF PRISM):


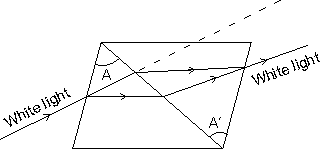
The emergent ray is undispersed. for this

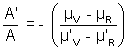
this is the condition for achromatism or no dispersion.

Why ??

Let µ'_V, µ'_R and µ be the corresponding values for the material of the second prism, while µ_V, µ_R & µ be of the first prism.

Angular deviation by first prism is
(_V - _R) = (µ_V - µ_R)A

Angular dispersion produced by second prism
('_V - '_R) = (µ'_V - µ'_R)A'

Since combination does not produce any dispersion
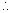(_V - _R) + ('_V - '_R) = 0

or A(µ_V - µ_R) + A'(µ'_V - µ'_R) = 0
or


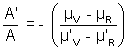
Illustration: Find the angle of a pism of dispersive power 0.021 and refrative index 1.53 to form on achromatic combination with the prism of angle 4.2⁰ and dispersive power 0.045 having refractive index 1.65. Also calculate the resultant deviation.

Solution: W = 0.021; µ = 1.53     W' = 0.045; µ' = 1.65
A' = 4.2 ⁰
For no dispersion
    W + W'' = 0
or W(µ - 1)A + W'(µ' - 1)A' = 0
or A = - 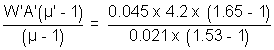= - 11.4⁰
Net deviation = + ' = (µ - 1)A + (µ' - 1)A'
                   = - 11.04⁰(1.53 - 1) + 4.2⁰(1.65 - 1) = - 3.12⁰


REFRACTION AT A SINGLE SPHERICAL SURFACE:

Consider a spherical surface of radius R separating two media with refractive indices µ₁ and µ₂ [the dig. is for the case µ₂ > µ₁]


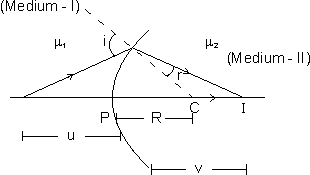
If µ is the object distance and v is the image distance, for light rays going from medium I to medium II, then

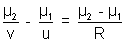
also transverse magnification in this case is
m =


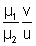
Dumb Question: Isthis equation valid for convex refracting surface ?

Ans: This equation is valid for all refracting surfaces convex, concave or plane. In case of plane refracting surface R .


Dumb Question: What sign convention is to be used ?

Ans: Sign convention remains same, as it was for mirror. All measurements are again to be done from P. While using this equation, the values of v, u and R with proper sign has to placed.

Why ??

here we rpove the formula for the case µ₁ < µ₂ however it holds for all cases for first refraction (at P).
µ₁ sin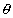₁ = µ₂ sin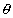₂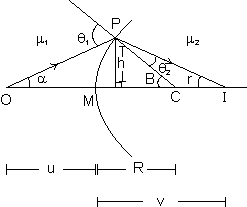


Assuming all angles to be very small, 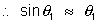   and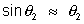
µ₁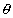₁ = µ₂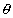₂ ....................................................... (i)

Using Geometry
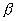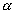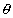+ = ₁ ....................................................... (ii)

[exterior angle theorem in POC]
II'ly 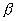   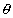= ₂ + 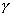............................................... (iii)

from (i), (ii) & (iii)
      µ₁( 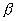+ 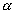) = µ₂( + )

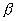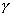=> µ₁ 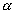+ µ₂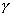 = (µ₂ - µ₁)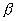
Here considering 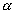, , 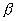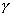to be small angle again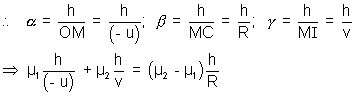


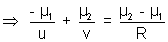
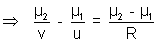    hence the equation.


Illustration: A transparent rod 40 cm long is cut at one end and rounded to a hemispherical surface 12 cm radius at the other end. A small object is embereded within the rod along its axis and half way between its ends. When viewed from the end of the rod, the object appears 12.5 cm deep. What is its apparent depth when the object viewed from curved end ?

Solution: Case - I: When the object viewed from the flat surface:


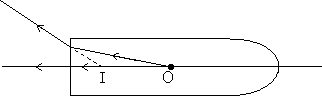
Real depth of the object = 20 cm
Apparent depth = 12.5 cm
Using µ = 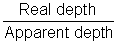   we have µ = 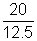= 1.6

Case - II: When the object is viewed the curved surface:


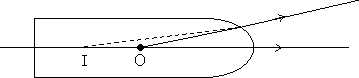
Here the refraction is taking place at the single curved surface. So we will use

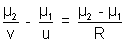
Here µ₁ = 1.6; µ₂ = 1; u = -2 cm; v = ? ; R = - 12 cm
So,
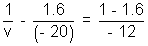
=> v = - 33.3 cm
Hence the object appears 33.3 cm deep from the curved surface.


THIN LENSES:

Lens: A lens is a transpsrent medium bounded by two refracting surfaces such that at least one of the refracting surfaces is curved