Geometric Optics - 6
SILVERING OF LENS:
Lens with silvered surface acts as a mirror. We can calculate the focal length of surface using
P = 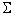 P1
P1
only modificaion is that power of mirror is given by Pmirror = 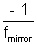
Dumb Question: How can be P = - 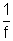 for a mirror be justified ?
for a mirror be justified ?
Ans: Focal length of concave mirror is -ve and for convex mirror it is +ve (as by our sign convention) But the nature of concave mirror is to converge the light and nature of convex is to diverge the light. If an optical system converges the light towards a point. Its power is assumed to be +ve (diverge being -ve). That’s why the formula for power in case of mirror is - 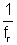 .
.
Dumb Question: How many times doeach individual poweris added ?
Ans: First the path of light is roughly determined. Then for each time ray passes (or gets reflected) through the element of system, then corresponding power is added.
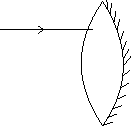
For example in the adjacant case the equation will be
Pnet = Plens + Pmirror + Plens
 light ray will have to pass through the lens surface twice (unsilvered).
light ray will have to pass through the lens surface twice (unsilvered).Illustration: A thin hollow equiconvex lens silvered at the back converges a parallel beam of light, at a distance of 0.2m in front of it. Where will it converge the same light, if filled with water (µ = 4/3).
Solution: When lens is hollow, it will simply act as concave mirror
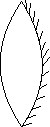
 Parallel beam is focussed atfocus of mirror only
Parallel beam is focussed atfocus of mirror only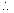 f = - 0.2 m (
f = - 0.2 m (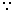 R = 2f = - 0.4 m)
R = 2f = - 0.4 m)When filled with water
Pnet = 2PL + PM = 2
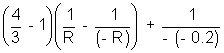
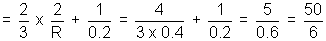
Now the complete system acts as mirror
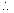 fnet =
fnet = 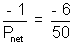 = - 0.12 m
= - 0.12 m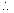 Parallel beam will now be focussed at a distance of 12 cm from the lens (on the side of object).
Parallel beam will now be focussed at a distance of 12 cm from the lens (on the side of object).PROBLEMS
Easy
1. A glass sphere of radius R = 10 cm is kept inside water. A point O is placed at 20 cm from A as shown in figure. find the position and nature of the image when seen from other side of the sphere. given µg = 3/L and µw = 4/3.
Solution: A ray of light starting from O gets refracted twice. The ray of light is travelling in a direction from left to right. Hence, the distance meausred in this direction are taken + ve.
Applying
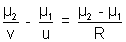 , twice with proper signs.
, twice with proper signs.we have,
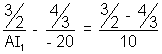 or AI1 = - 30 cm
or AI1 = - 30 cmNow, the first image I, acts as an object for the second surface, where
BI1 = u = - (30 + 20) = - 50 cm
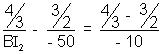
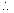 BI2 = 100 cm, i.e. the final image I2 is virtual andis formed at a distance 100 cm (towards left) from B.
BI2 = 100 cm, i.e. the final image I2 is virtual andis formed at a distance 100 cm (towards left) from B.Diagram
2. Focal length of a convex lens in air is 10 cm. find its focal length in water. (µg = 3/2 ; µw = 4/3)
Solution:
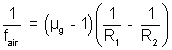 .............................................. (i)
.............................................. (i)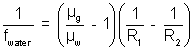 ........................................... (ii)
........................................... (ii)dividing equation (i) by (ii), we get
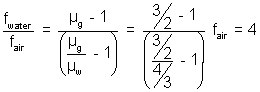
=> fwater = 4 fair = 4 x 10
= 40 cm
3. A spherical convex surface separates object and image space of refractive index 1.0 and 4/3. If radius of curvature of the surface is 10 cm, find its power.
Solution: For finding focus, we choose our object to be at
 , then image is formed at focus
, then image is formed at focusDiagram
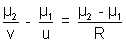
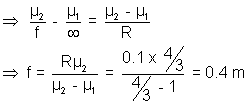
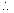 P =
P = 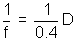
P = 2.5 dioptre
3. An isotropic point source is placed at a depth h below the water surface floating opaque disc is placed on the surface of water so that the bulb is not visible from the surface. What is the minimum radius of the disc. Take refractive index of water = µ.
Solutuion:
Diagram
Light from the source will not emerge out of waterif i >
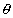 C
CTherefore, minimum radius R correspond to i =
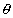 C
CIn
 SAB,
SAB,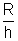 = tan
= tan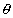 C
CR = h tan
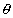 C
C 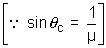
=
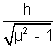
4. A pile 4m driver into the bottom ofa lake is 1m above the wate. Determine the length of the shadow of the pile on the bottom of the lake if the sum rays make an angle of 450 with the water surface. (µw = 4/3)
Solution:
Diagram
From Snell's law,
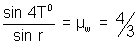
=> Sin r =
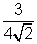
EF = DE tan r
= 3 tan(sin-1
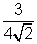 )
)= 1.88 m
 Total length of shadow L = CF
Total length of shadow L = CFL = (1 + 1.88)m = 2.88 m
5. The angle of minimum deviation for a glass prism with µ =
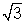 equaly the refracting angle of the prism. What is the angle of prism ?
equaly the refracting angle of the prism. What is the angle of prism ?Solution: Given A =
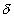 m
m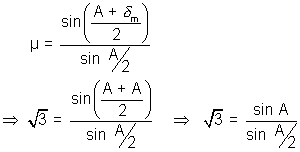
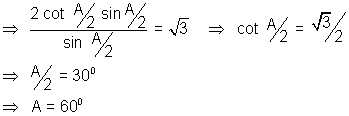
6. The angle of a prism are 300, 600 and 900. What should be the refractive index of a liquid to be kept in contact with the longest face so that a ray normally incident on the smallest face gets just internally reflected at the longest face ? (µ = 1.5)
Solution: The given prism ABC has the face AC the longest (opposite to 900 angle) and BC the shortest (opposite to 300 angle).
Diagram
PQ is the normally incident ray at the face BC and just gets totally reflected at the longest face AC.
For the glass-liquid interface AC
gµL =
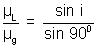
In
 CQD,
CQD,  CQD = 300
CQD = 300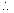
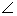 DQN = 600
DQN = 600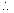 i = 600
i = 600 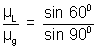
µL = µg sin 600 = 1.5 x
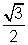 = 1.299
= 1.2997. A concave lens focusses a distant object 40 cm from it on a screen placed 10 cm away from it. A glass plate (µ = 1.5) and of thickness 3 cm is inserted between lens and a screen, where should the object be placed, so that its image is again focussed on the screen.
Solution:
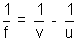
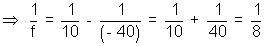
f = 8 cm
Diagram
Shift due to glass slab = t
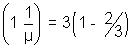
= 1 cm
For this position of object, image would have formed at 10 - 1 = 9 cm
if glass slab was not present
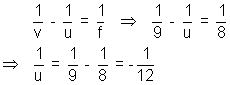
u = - 72 cm
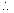 Object should be placed 72 cm from lens.
Object should be placed 72 cm from lens.8. Two plane concave lens of glass (µ = 3/2) have radius of curvature 20 & 30 cm, they are placed in contact with corved surface towards each iother and the space between them is filled with a liquid of refractive index 4/3. Find the focal length of the system.
Diagram
Solution: Pnet = P1 + P2 + P3
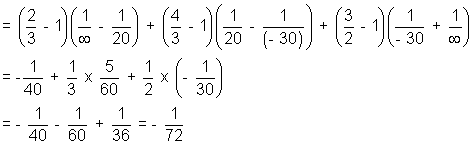
fnet =
 = - 72 cm (focal length of system)
= - 72 cm (focal length of system)9. A small fish 0.4 m below the surface of a leke is viewed through a simple converging lens of f = 3 m. The lens is kept at 0.2 m above the water surface such that the fish lie on the optical axis of the lens. Find the image of the fish seen by observer, the refractive index of water = 4/3.
Solution: Apparent depth of fish =
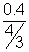 = 0.3
= 0.3Diagram
Apparent position of object = - (0.3 + 0.2) = - 0.5
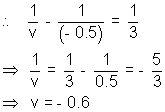
 image of the fish is formed at same point where fish is present.
image of the fish is formed at same point where fish is present.