Case II:
Field at internal point:
P is inside the sphere. Taking a small thin spherical shell of radius x and thickness dx[x < d]
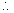
Field due to all such shell sun
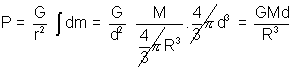
All shells having radius greater than P do not contribute to the field
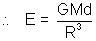Graphical representation of fields:
(i) Variation of gravitational field due to aring as a faver of its axial distance.
(ii) Gravitational field due to a uniform sphere
• As can be seen that the Gravitational field faver is continuous every where but is not differentiable at R.
°
Field due to uniform thin spherical shell
Case I: When point lies inside the spherical shell
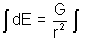
menclosed = 0, [
it is a shell i.e. hallow sphere]
Case II: When point P lies outside the spherical shell
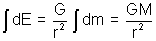
Thus for outide point, whole shell acts a point object located at the centre of sphere.
Graphical representation of field.
Dumb Question: How can the result I be justified physically ?
Ans:
We consider under whole shell to be made up of minute particles each of mass 'dm'. Then for any point P inside, the force diagram will be as shown in adjucant figure. Now since section
is smaller to P, hence force due to than will be stronger (as Force follows inverse square relation with distance] hence lesser particles with stronger force compensates more particles with weater force an left side.
Illustration: Two concentric shells of masses M
1 and M
2 are situated as shown in figure. Find the force on a particle of mass 'm' when the particle is located at (a) r = a (b) r = b (c) r = c. The distance r is measured from the centre of the shell.
Solution: We know that attraction at an external point due to spherical shell of mass M is
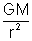
while at an internal point is zero.
So,
(a) For r = a, the point is external for both the shell; so
E
A =
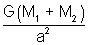
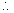
F
A = mE
A =
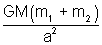
(b) For r = b, the point is external to the shell of mass M
2 and internal to the shell of mass M
1;
So,
E
B =
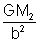
+ 0
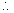
F
B = mE
B =
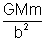
(c) For r = c, the point is internal to both the shells, so,
E
C = 0 + 0 = 0
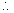
F
C = mE
C = 0
GRAVITATIONAL POTENTIAL:
Gravitational potential is defined for a point gravitational field. It is the work done by the external agent against the gravitational field in bringing unit mass from infinity to taht point without acceleration.
If work done is W then V =
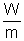
By the definition of potential energy u = W
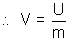
or U = mV
In differential term
V = -
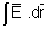
where
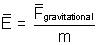
or E = -
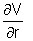Dumb Question: While defining potential, why the constraints of 'zero acceleration' been placed ?
Ans: Potential being defined for conservative forces, is actually the anount of work that has been done against and conservative force must be perfectly balanced and hence comes in the constraint of 'zero acceleration'.
