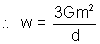Gravitation -3

GRAVITATIONAL POTENTIAL FOR FEW CASES:
• Gravitational potential at a point due to a point mass.

V = -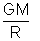

Why ??
Gravitational field due to a point mass is given by E = -

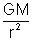
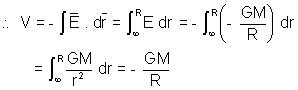
For all potential calculations, untill unless mentioned take zero of potential at infinity.

• Potential at a point due to a ring
at point P, it is given as
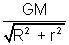
V = - , M = man of ring



• Due to spherical shell



Case I: Point P lies outside the shell V = -
Case II: Point P lies inside the shell V = -
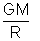
Graphical result can be shown as



• Potential due to homogenous solid sphere



Case I: when the point P lies outside the sphre
V = -
Case II: When the point P lies inside the sphere
V = -
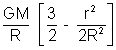
Graphical representation



Why ??
• Field due to a ring.



Let M be the mass and R be radius of a thin ring taking a small element of the eing and heating it as a point mass, the potential due to it is





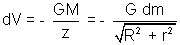
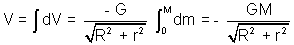GRAVITATIONAL POTENTIAL ENERGY:
Gravitational force is conservative and have potential energy is defined for it.
in previous section it was seen
    
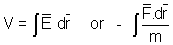
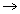
    V Potential at a point where 'm' is kept, due to all masses present.
or mV = -
    U = - = Vm



For two particles potential energy is given by Vm₂ = -

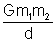Dumb Question: We know that potential energy is a relative term, however the formula above gives different inter pretation.
Solution: The above formula is for the case where the objects potential energy is calculated relative to zero point of potential energy.
The General formula should be
U_f - U_i = -
where U_f and U_i represents final and initial potential energy (w.r.t. zero point) and r₂ and r₁ represents the repective location of final and initial point.

Dumb Question: Is the force used in above formula external or gravitational ?
Solution: The force used in above formula is 'FORCE OF GRAVITATION'. If external force is given, then it can be used by just dropping the -ve sign of the formula and using rest of the things as it is, but the motion of the body must follow the constraight of 'ZERO ACCELERATION' if external force is being used using 'F_gravity' formula holds, irrecpective of acceleration.

ASSEMBLING A SYSTEM (POTENTIAL ENERGY OF A SYSTEM:
• If there is a system consisting of few objects, then the potential energy of complete system is same as the work done in assembling the system (with initially nothing present).

Illustration: Three particles each of mass m are placed at the corner of an euilateral triangle of side d. Calculate
(a) Work done in assembling the configuration.
(b) Work done on the system if the side of the triangle is changed from 'd' to '2d'.
Solution:



(a) Potential Energy of Complete System = U₁₂ + U₂₃ + U₃₁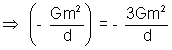


The work done in assembling the whole system will be same as this potenial energy.