The velocity of a satellite in its orbit is called orbiatry velocit. If V
0 is orbittal velocity then
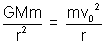
(for centripetal force balance)
=> v
0 =
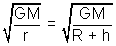
where h => height above ground
Dumb Question: What is the direction of this velocity ?
Ans: Orbitary velocity the velocity tangential to the path of motion of satellite. It is also independent of the mass of satellite.
• ENERGY OF SATELLITE
P.E. of a satellite = -
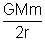
K.E. of a satellite =
mV
02 =
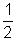
m
=
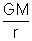
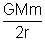
Total mechanical energy of satellite = P.E. + K.E.
= -
+
= -
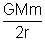
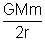Dumb Question: What is the significance of -ve total mechanical energy ?
Ans: Negative energy means that the satellite is bound to the central body by an attractive force and energy must be supplied to remove it from the orbit to infinity.
•
GEO-STATIONARY SATELLITE:
If there is a satellite rotating from west to east and havig same angular velocity a earths rotation, then such a satellite appers stationary from the orbit is called GEO-STATIONARY.
The orbit Geostationary satellite is called 'PRKING ORBIT'.
•
TIME PERIOD OF SATELLITE:
T =
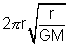
where r -> radius of orbit
M -> man of central planet
How ??
T =
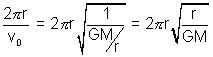
or T
2 =
KEPLER'S LAWS:
Kepler gave three empirical laws for the motions of planet around a central star(Sun)
(i) Each planet moves in an elliptical orbit, with at one focus of the ellipse.
(ii) The radius vector, drawn from the sum to a planet, sweeps out equal areas inequal time i.e. its a real velocity ( or area swept out by it per unit time) is constant.
= constant,
where A -> Area swept by vector.
L -> Angular momentum of planet
m -> man of planet
=> L = constant
(iii) The square of the planet's time period is proportional to the cube of te semi-major axis of its orbit.
T
2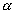 
a
3
Precisely T =
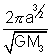
where M
5 = man of sun
• Important interpretation of IInd law
Let the area swept be shown in the adjucant figure.
dA =
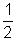
(base)(height) =
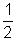
(SP)(P'M)
=
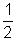
(r)(v sin
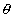
)dt
or
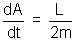
Since
= constant =>
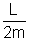
= constant
=> L = constant. Now
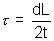
= 0
Now external torque acts on the system.
Dumb Question: What path will a particle follow. If give velocity v such that
(i) v < v
0 where v
0 = orbitary velocity.
(ii) v
0 < v < v
e v
e = escape velocity
(iii) v
e < v
Ans: (i) The path of particle is elliptical and it may or may not fall back on earth. If elliptical path crosses the earth, then it will fall back else not.
(ii) For V
0 < v < v
e, the particle will again follow elliptical path, but this time the point of projection is the nearest point from the focus, in the locus.
(iii) v > v
e, The path followed is hyperbolic while for v = v
e the path is parabolic.
Illustration: The mean distance of mass from the sun is 1.524 times that of the earth from the sun. Find the number of years required for mars to make on revolution about the sun.
Solution: For planets revolving around the sun T
2 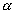r
3
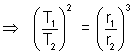
[T
1 : time-period of mars, T
2 : time-period of earth]
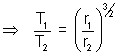
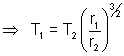
= (1)(1.524)
3/2 = 1.88 years
PROBLEMS:
Easy:
1. Complete the mass and density of the moon if acceleration due to gravity on its surface is 1.62 m/s
2 and radius is 1.74 x 10
6 (G = 6.67 x 10
-11)
Solution: We know that
g =
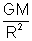
or M =
= 7.35 x 10
22Kg
Now P =
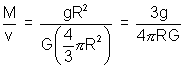
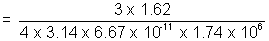
= 3.3 x 10
3 Kg/m
3
2. What will be the acceleration due to gravity on the surface of the moon if its radius 1/4 th the radius of the earth and mass 1/80th the mass of the earth. What will be the escape speed on the surface of the moon if it is 11.2 km/s on the surface of the earth.
Solution: As on the surface of planet
g =
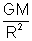
, we have
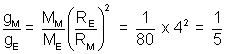
g
M = g
E/5 = 9.8/5 = 1.96 m/s
further as escape speed = v
e =
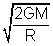
, So
v
M =
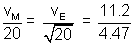
= 2.5 km/s
