3. The orbiatry velocity of an artificial satellite in a circular orbit just above earth's surface is v
0. What is the orbitary velocity for a satellite orbitary in a circular orbit at an attitude of half of earth's radius.
Solution: v
0 =
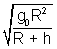
if h = 0 v
0 =
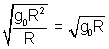
if h = R/2 v
0 =
=
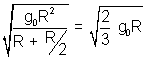
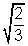
v
0
4. Find the gravitational force of attraction between a uniform sphere of mass M and a uniform rod length 'l' and mass 'm' oriented as shown in figure.
Solution: Since the sphere is uniform its entire mass may be considered to be concentrated at its centre. The force on elementary mass dm is
dF =
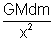
But dm =
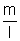
dx (thickness neglected)
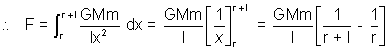
F =
=
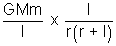
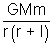
5. An orbitary satellite is moving in a circular orbit around the earth, with a speed equal to half the magnitude of escape velocity from earth.
Ditermine
(a) The height of satellite above earth's surface.
(b) If the satellite suddenly stops. Find the speed with it hit the earth's surface after falling down.
Solution: (a) v
e =
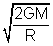
and v
0 =
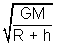
Now v
0 =
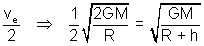
or 2(R + h) = 4R
=> h = R
(height of satellite above ground)
(b) If the satellite is stopped in orbit, the kinetic energy is zero and
Potetial Energy = -
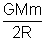
Total Energy = -
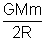
let velocity on reaching earth is 'v'
Potential Energy on the earth's surface = -
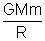
From conservation of mechanical energy
-
= -
+
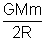
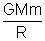
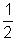
mv
2
or
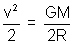
v =
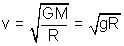
6. Suppose the earth increases its speed of rotation. At what new time period will the weight of a body in the equator becomes zero ?
(Take g = 10 m/s
2 and R
E = 6400 km)
Solution: The weight will become zero when g' = 0
also g' = g - Rw
2
=> g - Rw
2 = 0
=> w =
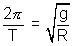
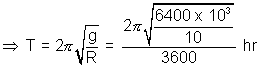
T = 1.4 hr
7. A particle of mass 1 Kg is kept on the surface of a uniform sphere of man m = 20 Kg and radius r = 1.0 m. Find the work to be done against the gravitational force between then to take the particle away from the sphere.
Solution: Potential at the surface of sphere,
v = -
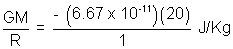
= - 1.334 x 10
-9 J/Kg
i.e. 1.334 x 10
-9 J work is obtained to bring a man of 1 Kg from
to the surface of sphere. Hence, the same amount of work will have to be done to take the particle away from the surface of the sphere.
Thus w = 1.334 x 10
-9 J
8. A planet of mass m revolves in elliptical orbit around the sun. So that its maximum and minimum distance from the sun are equal to r
a and r
p respectively. Find the angular momentum of this planet relative to the sun.
Solution: Using conservation of angular momentum
mv
pr
p = mv
ar
a
[As velocities or
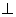
.... to the radius vector at apogee and perigee
=> v
pr
p = v
ar
a
Using conservation of energy
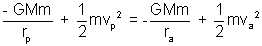
By solving the above equations,
v
p =
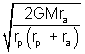
L = mv
pr
p = m
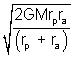MEDIUM:
1. Two bodies of masses M
1 and M
2 are placed at a distance d a point. What is the potential at the position where the gravittional field due to them is zero ?
Solution: Let the field be zero at a point distance x from M
1
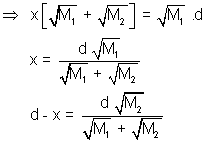
Potential at this point due to both the masses will be
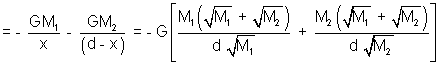
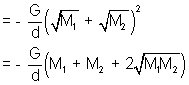
2. A rocket starts vertically with speed v
0. Show that its speed v at a height is given by v
02 - v
2 =
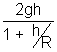
, where R is the radius of earth. Hence deduce the maximum height reached by the rocket fired with a speed of 90
0 of escape velocity.
Solution: Kinetic Energy on surface of earth =
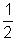
mv
02
