Potential Energy on surface of earth = -
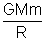
Total energy =

mv
02 -
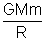
Kinetic Energy at a height h =

mv
2Potential Energy at this height = -
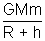
Total energy =

mv
2 -
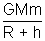
By the principle of conservation of energy

mv
2 -
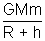
=

mv
02 -
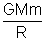

(v
02 - v
2) =
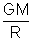
-
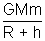
But GM = gR
2
(v
02 - v
2) =

v
02 - v
2 =
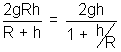
For maximum height v = 0
v
0 = 90% of escape speed = 0.9
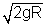
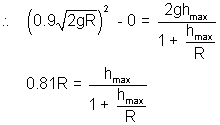
0.81R + 0.81h
max = h
max 0.19h
max = 0.81R
h
max =
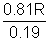
= 4.26R
3. Two satellites A and B of equal masses, move in the equitorial plane of earth, close to the earth's surface. Satellite A moves in the same direction as that of the rotation of earth while satellite B moves in the opposite direction. Determine the ratio of the kinetic energy of B to that of A in the reference frame fixed to earth (g = 9.8 m/s
2)
Solution:
Velocity of A with respect to earth =
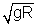
- wR
Velocity of B with respect to earth =
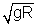
+ wR
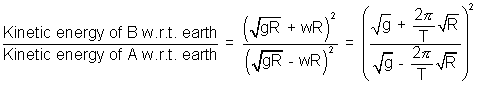
= 1.265
where T = 24 x 60 x 60 s R = 6400 x 10
3 m
HARD:
1. An artificial satellite of mass m of a planet of mass M, resolves in a circular orbit whose radius is n times the radius R of the planet. In the process of motion, the satellite experiences a slight resistance due to cosmic dust. Assuming resistance force on satellite depends on velocity as F = av
2 where a is constant. Calculate how long the satellite will stay in orbit before it falls onto the planet's surface.
Solution: Total energy in circular orbit of radius r,
E = -
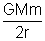
Rate of change of energy =
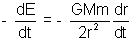
= F
resistiv. v = av
2.v = av
3also gravity provides the centripetal force
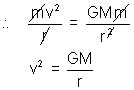
Now
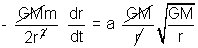
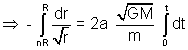
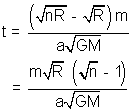
2. Find the maximum and minimum distances of the planet A from the sun S if at a certain moment of time it was a distance r
0 and travelling with the velocity vector being equal to

.
Solution:
At minimum and maximum distance velocity of satellite makes on angle of 90
0 with radius vector.
Applying conservation of angular momentum
mv
0r
0 sin

= mvr
By energy conservation

Solving equation (i) and (ii) we get two values of r, one is maximum distance another is minimum distance.
r
max =

r
min =
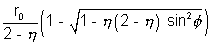
where
 Key words
Key words:
• Gravitational Force.
• Gravitationl Field.
• Gravitational Potential.
• Escape Speed.
• Orbittal Speed.
• Areal Velocity.
• Parking Orbit.