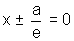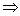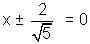Hyperbola - 1
Introduction
Hyperbola is a very important lonic section. It has a wide use in further engineering courses. Hyperbola is a very special curve which is very rarely seen in day to day life. The new concepts such as touching the curve at infinity fills us with a great excitement to read this chapter, so enjoy the curve named hyperbola by getting into the chapter and feel the touch of the line to the line to the curve at infinity. DEFINATION:
The locus of point which moves in a plane such that its distance from a fixed point called focus is e times (e > 1) its distance from a fixed line called directrix.
EQUATION OF HYPERBOLA
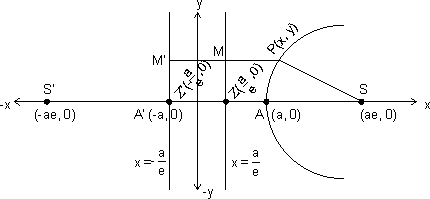
The standard equation of hyperbola is:
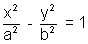
where b2 = a2(e2-1)
Why ?
Let s be the focus & ZM the directix of the hyperbola. Draw SZ
ZM & Divided SZ internally & externally in the ratio e:1 (e>1) & let A & A' be their internal & external points of division, then SA = eAZ & ...................(1)
SA'= eA'Z ........................(2)
Points A & A' will lie on the hyperbola. Let AA' = ZA & take C, the mid point of AA' of AA' as origin.
i.e. CA = CA' = a
Let P be any point on the hyperbola.
Then adding (1)& (2) we get
SA + SA' = e( AZ + A'Z)
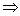(CS - CA) + (CS + CA') = eAA' 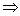2cs + CA' - CA = e(za)But CA' = CA, Hence
2CS = 2ae
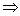CS = aeThus focus S is ( ae, 0)
Now subtrating (1) from (2) use get
SA'- SA = C(A'Z - AZ)
AA' = e[( CA' + CZ) - (CA - CZ)]
AA' = e[2CZ + CA' - CA]
But CA'= CA, then
2a = e(2cz)
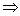CZ = a/eThus directrix is x = a/e
Now draw PM
MZWe know by the definaton of hyperbola, that
= SP = ePM
= (sp)2 = e2(pm)2
=
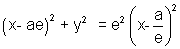
= (x - ae)2 + y2 = (ex - a)2
= x2 + a2e2 - 2aex + y2 = e2x2 + a2 - 2aex
= x2(e2 - 1) - y 2 = a2(e2 - 1)
=
=
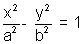
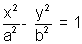
where b2 = a2(e2 - 1)
ILLUSTRATION : 1 .
Find the equation of hyperbola whose foci are (2, 4) & (10, 4) & eccentricity is 2.
Ans: We know that the center of hyperbola is the mid point of two foci i.e. coordinates of centers are (6, 4). We also know that the distance between two foci is 2ae.
i.e (10 - 2)2 + (4 - 4)2 = (zae)2
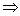2ac = 8 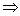4a = 8 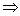a = 2b2 = a 2(e2 -1), Hence
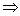a = 2 b2 = 4(4 - 1) = 12
The required equation of hyperbola is
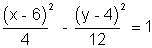
SOME TERM RELATED TO HYPERBOLA
(i) CENTER : This is the mid point of line joining the two foci. In standard form C is (0,0).
(ii) ECCENTRICITY : This is the ratio of the distances of any point on hyperbola from focus to the directrix. Here we have
& b2 = a2(e2 - 1)
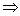e =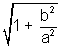 
(iii) FOCI: Foci consists of two points on the transvers axis of hyperbola whose mid point is the center of hyperbola. Coordinates: (Iae, 0)
(iv) DIRECTRICES : There are the two lines perpendicula to the transverse axis on oppsite sieds of centre. In standard form directrices are
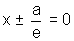
(v) AXES : In standard form points A(a,0) & A'(-a, 0) are called the vertices of hyperbola line AA' is called transverse axis & perpendicular to this is called conjugate axis.
(vi) DOUBLE ORDINATES : This is the length of the chord of hyperbola with end points as a, a', which is perpendicular to the transverse axis.
If the abscissa of Q is h then
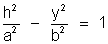
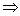
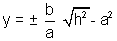
Hence coordinates of Q & Q' are
& 
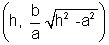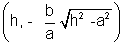.(vii) LATUS RECTUM: The double coordinates which pass through foci are called Latus rectums. The abscissa of Latus rectums are Iae. Hence the coordinates are
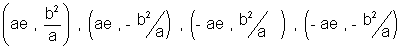, & the length of Lotus rectum is 
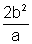.(viii) FOCAL CHORD : A chord of hyperbola that passes through focus is called the focal chord of hyperbola.
(ix) PARAMETRIC EQUATION OF HYPERBOLA: The parametric equations of given hyperbola
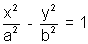are x = a sec
y = b tan
why ?
Let
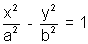be the hyperbola with centre C & transverse axis AA', Then the circle drawm with centre C & segment AA' as diameter is called auxiliary circle. Equation is: x2 + y 2 = a2
Let P be any point on hyperbola & Q on circle Draw PN perpendicular to axis & NQ be the tangent ot circle, then join CQ.
Let
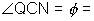eccentric angle of P since Q = (a cos
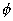, a sin ) x = CN = a sec
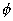
But P(x, y) lies on hyperbola, then
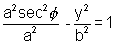
y = b tan Hence the parametric equations of hyperbola
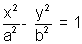are x= sec 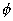, y = tan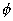 
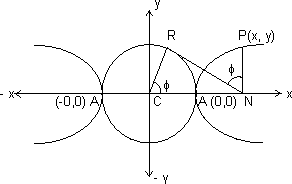
ILLUSTRATION : 2. Find the centre, foci, vertices, eccentricity, length, of axes, Latus Rectum & directrices of the hyperbola 3x2 - 2y2 + 12x + 4y + 4 =0
Ans: 3x2 - 2y2 + 12x + 4y + 4
= 3(x2 + 4x + 4 - 4) - 2 (y 2 - 2y + 1 - 1) + 4
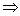3(x+2)2 - 12 - 2(y - 1)2 + 2 + 4 = 0 3(x + 2)2 - 2 (y - 1)2 = 6 
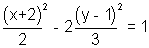
Centre = (- 2, 1)
Here a2 = 2
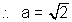
b2 = 3
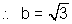
Hence
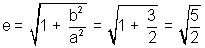
foci = (± ae, 0) =
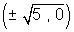
vertics = (± ae,0) =
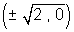
eceentricity =
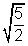
length of axex = 2a & 2b
=
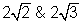
Latus Rectum =
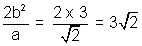
Directrices =
