Hyperbola - 2

FOCAL DISTANCES OF A POINT:

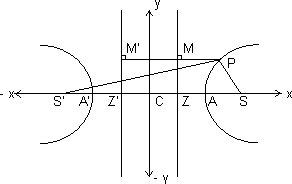
Another Defination of hyperbola is that the difference of focal distances of any point on hyperbola is constant & equal to the length of transverse axis of the hyperbola.

Why ?
Let the hyperbola be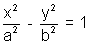  

We know that
Distance from focus = (Distance from Directrix)
Hence Distance of point P(x₁, y₂) from S,(ae,0) is
     SP = ePM = e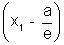 = ex₁ - a
Similarly S’P = e(PM’) = e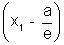 = ex₁ + a
Hence S’P - SP = 2a
                     = Transverse axis
Hence Hyperbola is the Locus of a point which moves in a plane such that the difference of its distances from two fixed points i.e. foci is constant.

POINT AND HYPERBOLA

The point (x₁, y₂) lies outside, on ,or inside the hyperbola 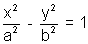accordingly as 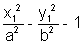< , = or > 0

Why ?
Let P = (x₁, y₂) & Q = (x₁ y₁)

Draw QL perpendicular to x axis then
     QL > PL
y₁ > y₂



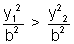
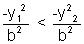
Adding on both sides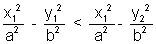
    
But
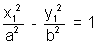
Hence

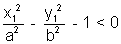
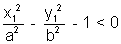
When point lies outside. Similarly we can prove that when point lies on of inside the hyperbola Then


LINE AND A HYPERBOLA

The line y = mx + c will cut the hyperbola in two points, one point or will not cut accordingly as c² >, = or < a²m² - b²

Why ?
Let the line be y = mx + c ……………………………………… (1)
& the hyperbola   …………………………………… (2)
Eliminating y form (1) & (2) we get
    
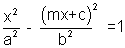
x²(a²m² - b²) + 2mca²x + a²(b² + c²) = 0
This is a quadratic is x, hence
Discriminant = b² - 4ac
                  = 4m²c²a⁴ - 4(a²m² - b²)(a²)(b² + c²)
                  = c² + b² - a²m²
Line will cut in two points if D > 0
c² + b² - a²m² > 0 c² >a²m² - b²
Line will touch the parabola if D = 0
i.e. c² + b² - a²m² = 0 c² = a²m² - b²

Line will not be touch or be touch a chord of parabola
if D < 0 i.e. c² + b² - a²m² < 0
c² < a²m² - b²


ILLUSTRATION : 3.
For what values of K will the line y = 3x + K be a chord to the hyperbola

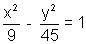
Ans: For this hyperbola we have
     a² = 9   &   b² = 45
From the equation of given line
     m = 3   &   c = k
Hence we know that for a line to be a chord to hyperbola c² > a²m² - b²
i.e. K² > 9 x 9 - 45
  K² > 36
  K² - 36 > 0
  (K - 6)(K + 6) > 0
Hence


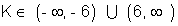
EQUATIONS OF TANGENT

(a) POINT FORM:
The equation of tangent to the hyperbola at (x ₁y₁) is
i.e. T = 0 where T =

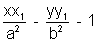
Why ?
The equation of hyperbola is:
    
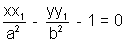
Differentiating w.r.t.x. we get
    

    

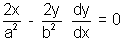
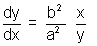
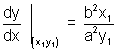
Equation of tangent when it passes through (x₁y₁) is
(y - y₁) =

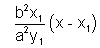
a²y₁y - a²y₁² = b²x₁x - b²x₁²
Dividing whole equation by a²b² we get
    

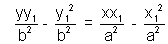
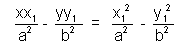
But 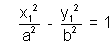as (x₁, y₁) lies on hyperbola
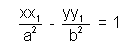is the requurired equation


(b) PARAMETRIC FORM:
The equation of tangent to hyperbola at
(a sec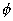, b tan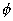) is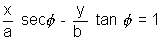
    

Why ?
We have to paranetric equations of hyperbola as
     x = a sec 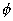& y = b tan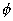
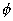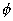Differentiating both equations we get dx = a sec tan d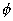 & dy = b sec² 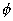d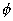
Hence dividing these equations we get,
  
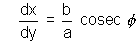
Hence the equations of tangent is (y - b tan) =
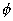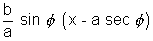
ay sin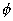cos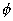 - ab sin² 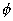= cos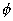bx - ab
say sin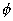 cos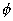 - bx cos 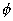= - ab cos²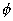


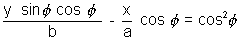
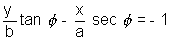
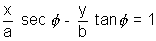  is required equation.


SLOPE FORM:
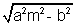The equations of tangent to the hyperbola of slope m is y = mx ± & coordinates of points of contact are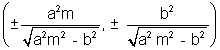
    

Why ?

Let the line with slope m be
     y = mx + c, tangent to
    
Eliminating y from these two equations we get
    (a²m² - b²)x² + 2 mca²x + a²(c² + b²) = 0
This is a quadratic equations in x hence for only one solution D should be zero.
  D = b² - 4ac = 4m²c²a⁴ - 4(a²m² - b²(a²b² + c²) = 0
c² = a²m² - b²
c =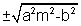
Hence the equation of tangent is:
     y = mx 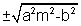……………………………. (1)
Now, we also know that the equation of tangent at (x₁, y₁) is
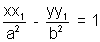     ………………………………….. (2)
Comparing (1) & (2) as they are the same equation we get
    
&
    
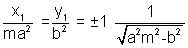
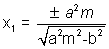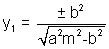
Hence the coordinates of point of contact are .
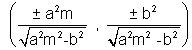