Hyperbola - 3

ILLUSTRATION : 4.
Find the equations of the tangent to the hyperbola 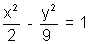which is perpendicular to the line 3y + x =1
Let the slope of line be m then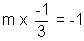
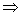m = 3
&  a² = 2   &   b² = 9
Hence equations of tangents are:
    
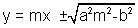
i.e. y = 3x +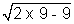
&   y = 3x -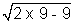
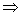equations are
     y = 3x + 3
&   y = 3x - 3


EQUATIONS OF NORMAL

(a) POINT FORM:

Equations of normal to the hyperbola 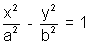at (x₁,y₁) is 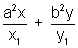= a² + b²

Why ?
The equations of hyperbola is
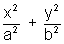     - 1 = 0
Differentiating w.r.t.x we get
    

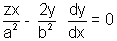
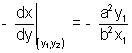
Hence the equation of normal is
    (y - y₁) = 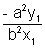(x - x₁)

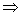b²x₁y - b²x₁y₁ = - a²y₁x + a²x₁y₁
Dividing whole equation by x₁y₁
    
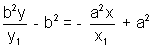
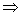
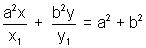is the required equation


(b) PARAMETRIC FORM:
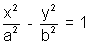The equation of normal at (a sec, tan) to the hyperbola is
     xa cos + by cot = a² + b²

Why ?
We know that the parametric equations of hyperbola are
     x = a sec     y = tan
Differentiating them we get
     dx = a sec tand   &   dy = bsec²d
Dividing them we get
    
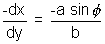
Hence the equation of normal is
     (y - b tan) = 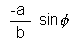(x - a sec)
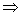by - b² tan = - ax sin + a²t an
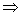ax sin + by = (a² + b²)tan
Dividing whole equation by tan we get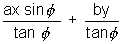
= a² + b²
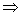as cos + by cot = a² + b² is required equation.


(c) SLOPE FORM:
The equations of the mormals of slope m to the hyperbola 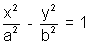are given by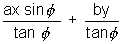

Why ?
We know that the equation of normal at (x₁, y₁) is 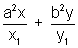= a² + b²
since m is the slope, then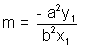


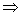
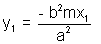
&   (x₁, y₁) lies on



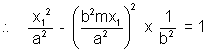
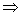
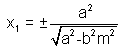
     y₁ = ±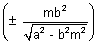
Hence the equation of normal in term of slope is
     y - 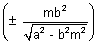= m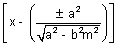
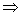y = mx ± 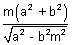is the required equation of normal in slope form.


Illustration : 5.
Find the equation of normal to 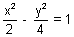at the poimt whose eccentric angle is .

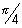Ans: We know the equation of normal in terms of eccentric angle is
     ax cos + by cot = a² + b²
Here   = 45⁰, a = 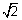, b = 2
  ax cos45⁰ + by cot45² = a² + b²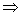
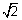.x.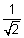 + 2.y.1 = 2 + 4
  x + 2y = 6   is the required equation.


EQUATION OF A CHORD BISECTED AT A GIVEN POINT:

The equation of a chord of hyperbola 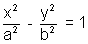, bisected at (x₁, y₁) is T = S₁ where   T = 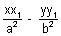- 1   &   S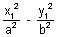₁ = - 1
i.e. =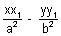

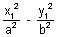
Why ?
Let QR be the chord whose mid point is P. Since Q & R lies on hyperbola.

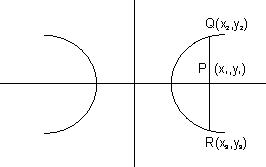
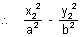= 1 .............................. (i)   & also
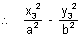= 1 .............................. (ii)
Subtracting (ii) from (i) we get
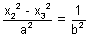     (y₂² - y₃²)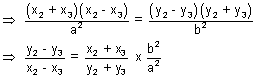


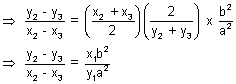
Hence slope of chord joining Q & R is
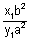
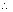  The equation of chord QR is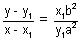
    
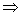yy₁a² - y₁²a² = xx₁b² - x₁²b²
Dividing whole equation by a²b² we get


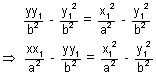
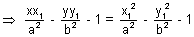
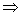T = S₁
is the required equation of chord with given mid point.


PAIR OF TANGENTS

The combined equation of pair of tangents drawn from a point (x₁, y₁) to the hyperbola 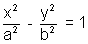is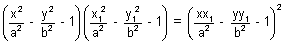
i.e.   SS₁ = T²
where S = 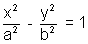; S₁ = 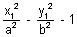; T =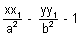

Why ?

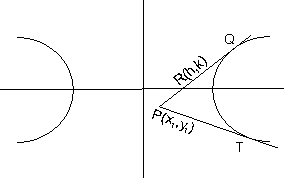
Let R(h, k) be any point on pair of tangents PQ or PT from any external point P(x₁, y₁) to the hyperbola .
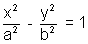Equation of PR is

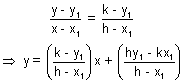
But this line is a tangent to the hyperbola so it must be of the form.
     y = mx ±
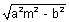
Here   c = 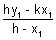  &   m =
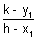
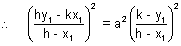- b²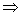
(hy₁ - kx₁)² = a²(k - y₁)² - b²(h - x₁)²

Hence locus of (h, k) is
     (xy₁ - yx₁)² = a²(y - y₁)² - b²(x - x₁)²

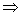(xy₁ -- yx₁)² = - (b²x² - a²y²) - (b²x₁² - a²y₁²) - 2(a²yy₁ - b²xx₁)

Dividing whole equation by a²b² we get

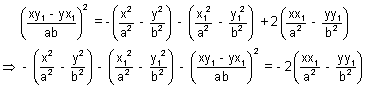
Adding 1 + 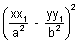on both sides we get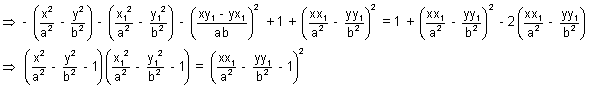

i.e.   SS₁ = T²