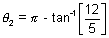Hyperbola - 4
Illustration : 6.
Find the equation of pair of tangents drawm from a point P(1, 1) to the hyperbola 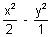 = 1.
= 1.
Ans: Here a2 = 2 b2 = 1
S = 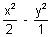 - 1
- 1
S1 = 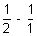 - 1 = -
- 1 = - 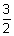
T = 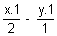 - 1 =
- 1 = 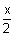 - y - 1
- y - 1
Hence equation is SS1 = T2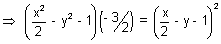
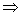 - 3(x2 - 2y2 - 2) = (x - 2y - 2)2
- 3(x2 - 2y2 - 2) = (x - 2y - 2)2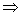 4x2 - 2y2 - 4x + 8y - 4xy - 2 = 0
4x2 - 2y2 - 4x + 8y - 4xy - 2 = 0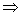 2x2 - y2 - 2x + 4y - 2xy - 1 = 0 is the equation of pair of tangents.
2x2 - y2 - 2x + 4y - 2xy - 1 = 0 is the equation of pair of tangents.
CHORD OF CONTACT:
If the tangent from a point P(x’, y’) to the hyperbola 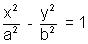 touch the equation of chord of contact QR is
touch the equation of chord of contact QR is
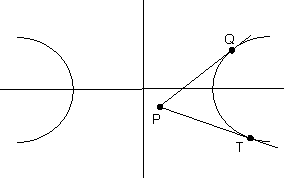
Why ?
Let Q = (x1, y1) & R = (x2, y2)
We know that PQ & Pr are tangents, hence equation of PQ is
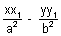 = 1 ......................................... (i)
= 1 ......................................... (i)equation of PR is
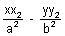 = 1 ........................................ (ii)
= 1 ........................................ (ii)Since both (i) & (ii) passes through P(x', y')
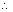
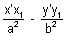 = 1 ........................................ (iii)
= 1 ........................................ (iii)&
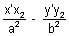 = 1 ........................................ (iv)
= 1 ........................................ (iv)By looking carefully at (iii) & (iv) we can say that (x1, y1) & (x2, y2) lies on
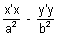 = 1 i.e. T = 0.
= 1 i.e. T = 0.POLE AND POLAR:
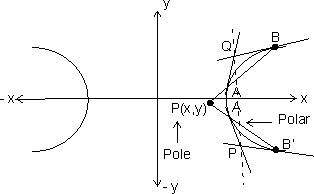
Let P(x1, y1) be any point inside or outside the hyperbola the if any straight line drawn through P intersects the hyperbola at A & B. Then the locus of points of intersection of tangents to the hyperbola at A & B is called the polar of the given point P with respect to hyperbola & the point P is called the pole of the polar.
Why ?
Let P be (x1, y1) & hyperbola be
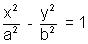 . If tangents to the hyperbola at A & B meets at Q(h, k), then AB is the chord ofcontact with respect to Q(h,k).
. If tangents to the hyperbola at A & B meets at Q(h, k), then AB is the chord ofcontact with respect to Q(h,k).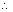 Equation of AB is
Equation of AB is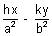
But P(x1, y1) lies on it, hence
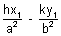 = 1
= 1Hence locus of Q(h, k) is
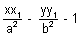
This is required equation of polar with (x1, y1) as its pole.
Illustration : 7.
Find the pole of given line y = mx + c with respect to hyperbola
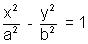 .
.Ans: Let the pole of line be (
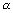 ,
, 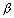 ) then the polar with respect to hyperbola is
) then the polar with respect to hyperbola is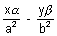 = 1
= 1But we have given the polar to be
y = mx + c
Hence by comparing the coefficients we get
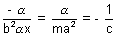
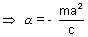 &
& 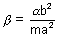
Hence pole is
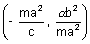
DEAMETER:
The locus of the middle points of any set of parallel chords of a hyperbola is called a diameter & the point where diameter intersects the hyperbola iscalled the vertex of diameter & equation of diameter is y =
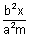 .
.Why ?
Let y = mx + c be a set of parallel chords with c as a variable.
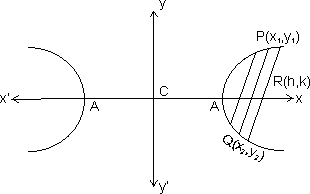
By solving y = mx + c , we get
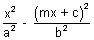 = 1
= 1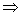 (a2m2 - b2)x2 + 2mca2x + a2(b2 + c2) = 0
(a2m2 - b2)x2 + 2mca2x + a2(b2 + c2) = 0This equation has roots x1 & x2
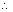 x1 + x2 =
x1 + x2 = 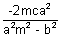 ......................................... (i)
......................................... (i)But (h, k) is the middle point of QR then,
h =
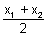 .................................................. (ii)
.................................................. (ii)From (i) & (ii)
h =
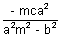
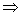 c =
c = 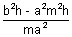
We also know that (h, k) lieson y = mx + c
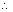 k = mh + c
k = mh + c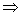 k = mh +
k = mh + 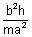 - mh
- mh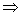 k =
k = 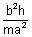 .
.CONJUGATE DIAMETERS
Two diameters are said to beconjugate when each bisects all chords parallel to the others.
Why ?
Let one set of parallell chords be
y = mx + c .............................................. (i)
then its diameter is y =
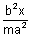
Let other set of parallel chords be
y = m1x + c
then its diameter is y =
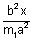 ........................ (ii)
........................ (ii)But slope of equation (i) & (ii) are same, therefore
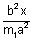 = m
= m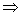 mm1 =
mm1 = 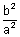
Therefore product of the slopes of two conjugate diameter is
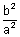 .
.Illustration : 8.
Find the condition for the lines 2Ax2 + 2Hxy + By2 = 0 to be conjugate diameter of
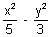 = 1.
= 1.Ans: Let the slope of lines whose equation is 2Ax2 + 2Hxy + By2 = 0 be m1 & m2 then we know that
m1m2 =
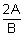 ........................................... (i)
........................................... (i)We also know that if m1 & m2 are the slopes of two conjugate diameters then
m1m2 =
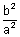 ........................................... (ii)
........................................... (ii)Hence by (i) & (ii)
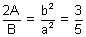
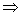 10A = 3B is the required condition.
10A = 3B is the required condition.DIRECTOR CIRCLE:
The locus of the point of intersection of the tangent to the hyperbola
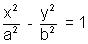 , which are perpendicular to each other is called director circle & the equation of director is
, which are perpendicular to each other is called director circle & the equation of director isx2 + y2 = a2 - b2 (a > b )
Why ?
The equation of tangent to hyperbola with slope m is
y = mx +
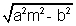 ................................... (i)
................................... (i)& the perpendicular tangent with slope -
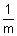 is
isy = -
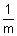 x +
x + 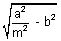 ................................... (ii)
................................... (ii)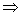 x + my =
x + my = 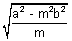 .................................... (iii)
.................................... (iii)Squaring & adding equations (i) & (iii) we get
(y - mx)2 + (x + my)2 = a2m2 - b2 + a2 - b2m2
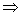 (1 + m2)(x2 + y2) = (1 + m2)(a2 - b2)
(1 + m2)(x2 + y2) = (1 + m2)(a2 - b2)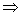 (1 + m2)[x2 + y2 - (a2 - b2)] = 0
(1 + m2)[x2 + y2 - (a2 - b2)] = 0As 1 + m2
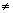 0, therefore
0, thereforex2 + y2 = a2 - b2 is the equation of director circle of hyperbola.
Illustration : 9.
Find the radius of the director circle of the hyperbola
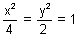 .
.Ans: We know the equation of director circle of is
x2 + y2 = a2 - b2
Here a2 = 4 & b2 = 2
Therefore x2 + y2 = 4 - 2 = 2
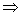 x2 + y2 = (
x2 + y2 = (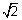 )2 = r2
)2 = r2Here r =
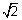 , Hence the radiusof director circle is
, Hence the radiusof director circle is 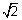 units.
units.ASYMPTOTES
An asymptote of a hyperbola or any curve is a straight line which touches the curve at infinity at two points. The equation of asymptotes is y = ±
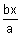
Why ?
Let y = mx + c be an asymptote to
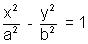
Hence solving bot we get
(a2m2 - b2)x2 + 2a2mcx + a2(b2 + c2) = 0
Now thishas two solutions for x & the asymptote touches the hyperbola at
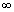 therefore both the roots must be
therefore both the roots must be 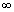 . By looking at the above equation the only way that
. By looking at the above equation the only way that 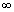 can be a solution is to be zero. Therefore
can be a solution is to be zero. Thereforea2m2 - b2 = 0 & 2a2mc = 0
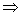 m = ±
m = ± 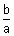 & c = 0
& c = 0Substituting m & c in y = mx + c
We get
y = ±
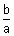 x is the required equation of asymptotes.
x is the required equation of asymptotes.Illustration : 10.
Find the angle between asymptotes of hyperbola
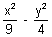 = 1.
= 1.Ans: THe equation of asymptotes is
y = ±
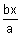 = ±
= ± 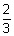
Now we have to find angle between two lines
y =
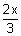 & y = -
& y = - 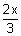
If m1 & m2 are slopes than angle between them is
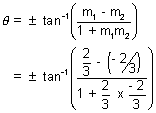
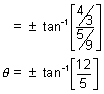
Hence the acute angle between the asymptotes is
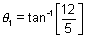
& the obstuse angle is